Matematik tarihi
Matematik tarihi, öncelikle matematikteki keşiflerin kökenini araştıran ve daha az ölçüde ise matematiksel yöntemleri ve geçmişin notasyonunu araştıran bir bilimsel çalışma alanıdır. Modern çağdan ve dünya çapında bilginin yayılmasından önce, yeni matematiksel gelişmelerin yazılı örnekleri yalnızca birkaç yerde gün ışığına çıktı. MÖ 3000'den itibaren Mezopotamya eyaletleri Sümer, Akad ve Asur, Eski Mısır ve Ebla ile birlikte vergilendirmede, ticarette, doğayı anlamada, astronomide ve zamanı kaydetmede/takvimleri formüle etmede aritmetik, cebir ve geometri kullanmaya başladı.
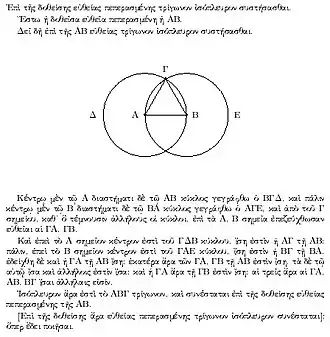
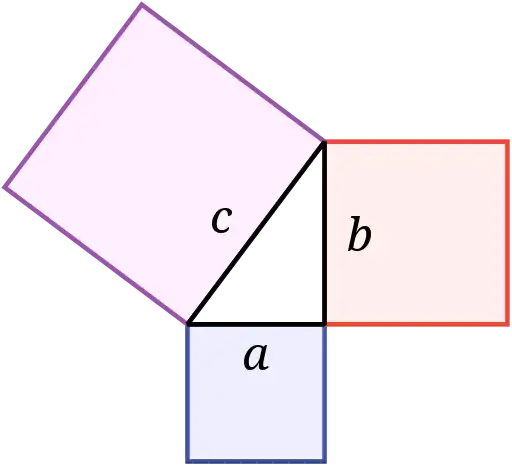
Günümüzdeki en eski matematiksel metinler Mezopotamya ve Mısır'dandır; Plimpton 322 (Babil, y. MÖ 1900)[2], Rhind Papirüsü (Mısır, y. MÖ 2000–1800)[3] ve Moskova (Golenischev) Papirüsü (Mısır, y. MÖ. 1890). Tüm bu metinler, Pisagor üçlülerinden bahseder. Bu nedenle, çıkarım yoluyla Pisagor teoremi, temel aritmetik ve geometriden sonra en eski ve yaygın matematiksel gelişme olarak görülmektedir.
Matematiğin bir "belirtici disiplin" olarak incelenmesi, MÖ 6. yüzyılda "matematik" terimini "eğitim konusu" anlamına gelen eski Yunanca μάθημα'dan (mathema) türeten Pisagorcularla başlar.[4] Yunan matematiği, yöntemlerini büyük ölçüde geliştirdi (özellikle tümdengelimli akıl yürütme ve kanıtlarda matematiksel kesinlik yoluyla) ve matematiğin konusunu genişletti.[5] Teorik matematiğe neredeyse hiç katkı sağlamamış olsalar da, eski Romalılar uygulamalı matematiği ölçme, yapı mühendisliği, makine mühendisliği, defter tutma, ay ve güneş takvimlerinin oluşturulması ve hatta güzel sanatlar ve el sanatlarında kullandılar. Çin matematiği, basamak değeri sistemi ve negatif sayıların ilk kullanımı da dahil olmak üzere matematiğe erken dönemde katkı vermiştir.[6][7] Hint-Arap rakam sistemi ve bugün dünya genelinde kullanılan işlemlerinin kullanımına ilişkin kurallar, Hindistan'da MS birinci bin yıl boyunca gelişti ve Muhammed ibn Mūsā el-Harezmi'nin çalışmasıyla İslam matematiği yoluyla Batı dünyasına aktarıldı.[8][9] İslam matematiği de bu medeniyetler tarafından bilinen matematiği geliştirdi ve genişletti.[10] Bu kültürel mirasla eşzamanlı fakat onlardan bağımsız olan, Meksika ve Orta Amerika'daki Maya uygarlığı tarafından geliştirilen, Maya rakamlarında sıfır kavramına standart bir sembol verilen matematikti.
Matematikle ilgili birçok Yunanca ve Arapça metin, 12. yüzyıldan itibaren Ortaçağ Avrupa'sında matematiğin daha da gelişmesine yol açacak şekilde Latince'ye çevrildi. Antik çağlardan Orta Çağ'a kadar, matematiksel keşif dönemlerini genellikle yüzyıllar süren durgunluk takip etti. 15. yüzyılda Rönesans İtalyasından başlayarak, yeni bilimsel keşiflerle etkileşime giren yeni matematiksel gelişmeler, günümüze kadar artan bir hızla devam etti. Bu, hem Isaac Newton hem de Gottfried Wilhelm Leibniz'in 17. yüzyıl boyunca sonsuz küçükler hesabının gelişiminde çığır açan çalışmasını içerir. 19. yüzyılın sonunda Uluslararası Matematikçiler Kongresi kuruldu.[11] Kongre, dört yılda bir dünyanın farklı ülkelerinden matematikçileri bir araya getirerek bu alandaki gelişmelere destek vermeye devam ediyor. Her kongrede matematiğe değerli katkılar sunan matematikçilere, Fields Madalyası, Nevanlinna Ödülü, Gauss Ödülü ve Chern Madalyası verilir.[11]
Tarih öncesi
Matematiksel düşüncenin kökenleri sayı, doğadaki örüntüler, büyüklük ve biçim kavramlarına dayanır.[12] Hayvan bilişiyle ilgili modern çalışmalar, bu kavramların insanlara özgü olmadığını göstermiştir. Bu tür kavramlar, avcı-toplayıcı toplumlarda günlük yaşamın bir parçası olabilirdi. Zaman içinde yavaş yavaş gelişen "sayı" kavramı fikri, "bir", "iki" ve "çok" arasındaki ayrımı koruyan, ancak ikiden büyük sayıları ayırmayan dillerin varlığı tarafından desteklenmiştir.[12]
Afrika'da keşfedilen, 20.000 yıllık veya daha eski tarih öncesi eserler, zamanı ölçmek için erken girişimlere işaret etmektedir.[13] Nil Nehri'nin (kuzeydoğu Kongo) kaynak sularının yakınında bulunan Ishango kemiği[14], 20.000 yıldan daha eski olabilir ve kemiğin uzunluğu boyunca uzanan üç sütuna oyulmuş bir dizi işaretten oluşur. Yaygın yorumlar, Ishango kemiğinin ya asal sayı dizilerinin[15] bilinen en eski gösteriminin bir çetelesini ya da altı aylık bir ay takvimini gösterdiği şeklindedir.[16] Peter Rudman, asal sayılar kavramının gelişiminin ancak MÖ 10.000 sonrasına tarihlenen bölme kavramından sonra ortaya çıkabileceğini ve asal sayıların muhtemelen MÖ 500 yılına kadar anlaşılmadığını savunuyor. Ayrıca, "bir şeyin çetelesinin neden ikinin katları, 10 ile 20 arasında asal sayılar ve neredeyse 10'un katları olan bazı sayılar göstermesi gerektiğini açıklamak için hiçbir girişimde bulunulmadığını" yazar.[17] Bilim adamı Alexander Marshack'a göre Ishango kemiği, Mısır'da matematiğin sonraki gelişimini etkilemiş olabilir, çünkü Ishango kemiğindeki bazı girişler gibi, Mısır aritmetiği de 2 ile çarpma işleminden yararlanmıştır; ancak bu tartışmalıdır.[18]
MÖ 5. bin yılın hanedanlık öncesi Mısırlıları, resimli olarak geometrik tasarımları temsil ediyordu. İngiltere ve İskoçya'da MÖ 3. bin yıldan kalma megalitik anıtların tasarımlarında daire, elips ve Pisagor üçlüleri gibi geometrik fikirleri içerdiği iddia edildi.[19] Bununla birlikte, yukarıdakilerin tümü tartışmalıdır ve şu anda tartışmasız en eski matematiksel belgeler, Babil ve Mısır hanedanlığı kaynaklarındandır.[20]
Babil
Babil matematiği, Mezopotamya (modern Irak) halklarının, Sümerlerin ilk dönemlerinden Helenistik döneme kadar neredeyse Hristiyanlığın şafağına kadarki dönemdeki tüm matematiğini ifade eder.[21] Babil matematik çalışmalarının çoğu, birbirinden geniş bir biçimde ayrılmış iki dönemden gelmektedir: MÖ 2. bin yılın ilk birkaç yüz yılı (Eski Babil dönemi) ve MÖ birinci bin yılın son birkaç yüzyılı (Seleukos dönemi).[22] Çalışma yeri olarak Babil'in merkezi rolü nedeniyle Babil matematiği olarak adlandırılmıştır. Daha sonra Arap İmparatorluğu döneminde Mezopotamya, özellikle Bağdat, bir kez daha İslam matematiği için önemli bir çalışma merkezi haline gelmiştir.

Mısır matematiğindeki kaynakların seyrekliğinin aksine, Babil matematiği hakkındaki bilgilerimiz 1850'lerden beri ortaya çıkarılan 400'den fazla kil tabletten elde edilmektedir.[23] Çivi yazısı ile yazılan tabletler, kil nemliyken yazılıp bir fırında veya güneşin ısısıyla sertçe pişiriliyordu. Bunlardan bazıları notlandırılmış ev ödevleri gibi görünmektedir.[24]
Yazılı matematiğin en eski kanıtı, Mezopotamya'daki en eski uygarlığı inşa eden eski Sümerler'e dayanır. MÖ 3000'den itibaren karmaşık bir metroloji (ölçme bilimi) sistemi geliştirdiler. MÖ 2500'den itibaren Sümerler kil tabletler üzerine çarpım tabloları yazdılar, geometrik egzersizler ve bölme problemleriyle uğraştılar. Babil rakamlarının en eski izleri de bu döneme aittir.[25]

Babil matematiği seksagesimal (altmışlık) sayı sistemi kullanılarak yazılmıştır.[23] Bundan türetilerek, dakikada 60 saniye, saatte 60 dakika ve bir daire içinde 360 (60 × 6) derecenin yanı sıra bir derecenin parçalarını belirtmek için yayın dakika ve saniyelerinin kullanılması gibi modern günlük kullanımlar elde edilir. Muhtemelen altmışlık sistem seçilmiştir çünkü 60, 2, 3, 4, 5, 6, 10, 12, 15, 20 ve 30'a eşit olarak bölünebilir.[23] Ayrıca, Mısırlılar, Yunanlar ve Romalılardan farklı olarak, Babilliler, sol sütuna yazılan rakamların ondalık sistemde olduğu gibi daha büyük değerleri temsil ettiği gerçek bir basamak-değer sistemine sahipti.[22] Babil notasyon sisteminin gücü, kesirleri tam sayılar kadar kolay bir şekilde temsil etmek için kullanılabilmesinden kaynaklanıyordu; böylelikle kesir içeren iki sayının çarpılması, modern gösterimimize benzer şekilde tam sayıları çarpmaktan farklı değildi.[22] Babillilerin notasyon sistemi, Rönesans'a[26] kadar herhangi bir medeniyetin en iyisiydi ve gücü dikkate değer hesaplama doğruluğuna ulaşmasına izin verdi; örneğin, Babil tableti YBC 7289, beş ondalık basamak doğrulukla √2'nin bir yaklaşık değerini verir.[26] Bununla birlikte, Babilliler ondalık virgülün eşdeğerinden yoksundu ve bu nedenle bir sembolün yer değerinin genellikle bağlamdan çıkarılması gerekiyordu.[22] Seleukos dönemine gelindiğinde, Babilliler boş pozisyonlar için yer tutucu olarak sıfır sembolü geliştirmişlerdi; ancak bu sadece ara pozisyonlar için kullanıldı.[22] Bu sıfır işareti uç konumlarda görünmüyor, bu nedenle Babilliler yaklaştılar ancak gerçek bir basamak değeri sistemi geliştirmediler.[22]
Babil matematiğinin kapsadığı diğer konular arasında kesirler, cebir, ikinci dereceden ve kübik denklemler ile düzenli karşıt çiftlerin (x, 1/x) hesaplanması yer alır.[27] Tabletler aynı zamanda çarpım tablolarını ve doğrusal, ikinci dereceden denklemleri ve kübik denklemleri çözmek için yöntemler içerir, bu o zaman için dikkate değer bir başarıdır.[28] Eski Babil dönemine ait tabletler, Pisagor teoreminin bilinen en eski ifadesini de içerir.[29] Bununla birlikte, Mısır matematiğinde olduğu gibi, Babil matematiği de kesin ve yaklaşık çözümler arasında fark veya bir problemin çözülebilirliği konusunda hiçbir farkındalık göstermez. En önemlisi, kanıtlara veya mantıksal ilkelere ihtiyaç olduğuna dair açık bir ifade yer almaz.[24]
Mısır

Mısır matematiği, Mısır dilinde yazılmış matematiği ifade eder. Helenistik dönemden itibaren Yunanca, Mısırlı bilginlerin yazı dili olarak Mısır dilinin yerini aldı. Mısır'da matematiksel çalışma daha sonra Arap İmparatorluğu altında İslam matematiğinin bir parçası olarak devam etti ve Arapça, Mısırlı bilim adamlarının yazı dili haline geldi.
En kapsamlı Mısır matematiksel metni Rhind Papirüsüdür (bazen yazarından dolayı Ahmes Papirüsü olarak da adlandırılır), y. MÖ 1650'e tarihlendirilir, ancak muhtemelen Orta Krallık'tan MÖ 2000-1800 yılları arasındaki eski bir belgenin kopyasıdır.[30] Aritmetik ve geometri alanındaki öğrenciler için bir kullanım kılavuzudur. Alan formülleri ve çarpma, bölme ve birim kesirlerle çalışma yöntemleri vermenin yanı sıra, aynı zamanda bileşik ve asal sayılar da dahil olmak üzere[31] diğer matematiksel bilgilerin kanıtlarını içerir; aritmetik, geometrik ve harmonik ortalamalar ve hem Eratosthenes Kalburunun hem de mükemmel sayı teorisinin (yani örneğin 6 sayısının) basit bir anlatımıdır.[32] Ayrıca, birinci dereceden doğrusal denklemlerin[33], aritmetik ve geometrik serilerin[34] nasıl çözüleceğini gösterir.
Bir diğer önemli Mısır matematiksel metni, Orta Krallık döneminden gelen ve y. MÖ 1890'e[35] tarihlendirilen Moskova Papirüsüdür. Bugün kelime problemleri veya hikâye problemleri olarak adlandırılan ve görünüşe göre eğlence amaçlı olan problemlerden oluşur. Kesik bir piramidin (frustum) hacmini bulmak için bir yöntem sağladığı için içerdiği bir problemin özellikle önemli olduğu düşünülmektedir.
Son olarak, Berlin Papirüsü 6619 (MÖ 1800), eski Mısırlıların ikinci dereceden bir cebirsel denklemi çözebileceklerini göstermektedir.[36]
Yunan
Yunan matematiği, Miletli Thales zamanından (y. MÖ 600), MS 529'da Atina Akademisi'nin kapatılmasına kadar Yunan dilinde yazılmış matematiği ifade eder.[37] Yunan matematikçiler, İtalya'dan Kuzey Afrika'ya tüm Doğu Akdeniz'e yayılmış şehirlerde yaşadılar, ancak kültür ve dil etrafında birleştiler. Büyük İskender'i izleyen dönemin Yunan matematiğine bazen Helenistik matematik denir.[38]
Yunan matematiği, daha önceki kültürler tarafından geliştirilen matematikten çok daha karmaşıktı. Günümüze ulaşan tüm Yunan öncesi matematiğin kayıtları, tümevarımlı akıl yürütmenin, yani pratik kuralları oluşturmak için kullanılan tekrarlanan gözlemlerin kullanımını göstermektedir. Yunan matematikçiler, aksine, tümdengelimli akıl yürütmeyi kullandılar. Yunanlar, tanımlardan ve aksiyomlardan sonuçlar çıkarmak için mantığı kullandılar ve bunları kanıtlamak için matematiksel kesinliği kullandılar.[39]
Yunan matematiğinin, Miletli Thales (MÖ 624 – y. 546) ve Samoslu (Sisamlı) Pisagor (MÖ 582 – 507) ile başladığı düşünülmektedir. Etkisinin kapsamı tartışmalı olsa da, muhtemelen Mısır ve Babil matematiğinden ilham almışlardır. Efsaneye göre Pisagor, Mısırlı rahiplerden matematik, geometri ve astronomi öğrenmek için Mısır'a gitmiştir.
Thales, piramitlerin yüksekliğini ve gemilerin kıyıdan uzaklığını hesaplamak gibi problemleri çözmek için geometri kullandı. Thales teoreminin dört sonucunu türeterek, geometriye uygulanan tümdengelimli akıl yürütmenin ilk kullanımı ona atfedilir. Sonuç olarak, ilk gerçek matematikçi ve matematiksel bir keşfin atfedildiği bilinen ilk kişi olarak selamlanmıştır.[40] Pisagor, doktrini "Matematik evreni yönetir" ve sloganı "Her şey sayıdır" olan Pisagor Okulu'nu kurdu.[41] "Matematik" terimini icat eden ve sadece matematik yapmak için matematik çalışmasını başlatan Pisagorculardı. Pisagor teoreminin ilk ispatı[42], teoremin uzun bir geçmişi olmasına ve irrasyonel sayıların varlığının kanıtı olmasına rağmen Pisagorculara atfedilir..[43][44] Öncesinde Babilliler ve Çinliler[45] olmasına rağmen, yeni Pisagorcu matematikçi Nicomachus (MS 60-120) en eski Greko-Romen çarpım tablolarından birini sunarken, en eski Yunan çarpım tablosu da MS 1. yüzyıla aittir (şimdi British Museum'da bulunmaktadır).[46] Yeni Pisagorcuların çarpım tablosunun Batı icadı ile olan ilişkisi, tablonun daha sonra Ortaçağ dönemindeki adında; mensa Pythagorica 'da açıkça görülmektedir.[47]
Platon (MÖ 428/427 - 348/347), başkalarına ilham vermek ve onlara rehberlik etmek açısından matematik tarihinde önemlidir.[48] Atina'daki Platonik Akademisi, MÖ 4. yüzyılda dünyanın matematik merkezi oldu ve Knidoslu Eudoxus gibi günün önde gelen matematikçileri bu okuldan geldi.[49] Platon ayrıca matematiğin temellerini tartışmış[50], bazı tanımları (örneğin "genişliği olmayan uzunluk" olarak bir doğru) netleştirmiş ve varsayımları yeniden düzenlemiştir.[51] Analitik yöntem Platon'a atfedilirken, Pisagor üçlülerini elde etmek için kullanılan bir formül onun adını taşır.[49]
Eudoxus (MÖ 408 – y. 355), modern integralin[52] bir öncüsü olan tükenme yöntemini ve ölçülemez büyüklükler[53] sorununu önleyen bir oranlar teorisini geliştirdi. İlki, alanların ve eğrisel şekillerin hacimlerinin hesaplanmasına izin verirken[54], ikincisi sonraki geometri uzmanlarının geometride önemli ilerlemeler kaydetmesini sağladı. Belirli bir teknik matematiksel keşif yapmamış olmasına rağmen, Aristoteles (MÖ 384 – y. 322) mantığın temellerini atarak matematiğin gelişimine önemli ölçüde katkıda bulundu.[55]
MÖ 3. yüzyılda, matematik eğitiminin ve araştırmanın önde gelen merkezi İskenderiye Okulu'ydu.[57] Öklid'in (y. MÖ 300), tüm zamanların en başarılı ve etkili ders kitabı olarak kabul edilen Elemanları yazdığı ve öğrettiği yer orasıydı.[1] Elemanlar matematiksel kesinliği aksiyomatik yöntemle tanıttı ve bugün hala matematikte kullanılan biçimin, tanım, aksiyom, teorem ve ispat biçiminin en eski örneğidir. Elemanlar adlı eserin içeriğinin çoğu zaten bilinmesine rağmen, Öklid bunları tek, tutarlı bir mantıksal çerçeve içinde düzenledi.[58] Elemanlar, 20. yüzyılın ortalarına kadar Batı'daki tüm eğitimli insanlar tarafından biliniyordu ve içeriği bugün hala geometri derslerinde öğretiliyor.[59] Öklid geometrisinin tanıdık teoremlerine ek olarak, Elemanlar, ikinin karekökünün irrasyonel olduğuna ve sonsuz sayıda asal sayı olduğuna dair kanıtlar dahil sayı teorisi, cebir ve katı cisim geometrisi[58] gibi zamanın tüm matematiksel konularına giriş niteliğinde bir ders kitabı anlamına geliyordu. Öklid ayrıca konik kesitler, optik, küresel geometri ve mekanik gibi diğer konularda da kapsamlı eserler yazdı, ancak yazılarının yalnızca yarısı günümüze ulaştı.[60]
Yaygın olarak antik çağın en büyük matematikçisi olarak kabul edilen Syracuse'li Arşimet (MÖ 287-212)[61], bir parabol yayının altındaki alanı, modern analizden çok farklı olmayan bir biçimde sonsuz bir serinin toplamı ile hesaplamak için tükenme yöntemini kullandı.[62] Ayrıca, π değerini istenen kesinlikte hesaplamak için tükenme yönteminin kullanılabileceğini gösterdi ve o zaman bilinen en doğru π değerini elde etti, 31071 < π < 31070[63]. Ayrıca kendi adını taşıyan sarmal, dönme yüzeylerinin (paraboloid, elipsoid, hiperboloid) hacimleri için elde edilen formüller[62] ve çok büyük sayıları ifade etmek için ustaca bir üs alma yöntemi üzerine çalışma yaptı.[64] Ayrıca fiziğe ve birkaç gelişmiş mekanik cihaza yaptığı katkılarla bilinmesine rağmen, Arşimet kendi düşüncesinin ürünlerine ve genel matematiksel ilkelere çok daha fazla değer verdi.[65] Küreyi çevreleyen bir silindirin yüzey alanı ve hacminin 2/3'ü olduğunu ispatlayarak elde ettiği bir kürenin yüzey alanı ve hacmine ilişkin bulgusu, en büyük başarısı olarak takdir edilmektedir.[66]
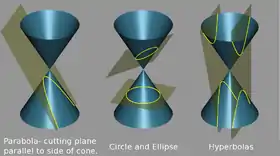
Pergeli Apollonius (MÖ 262–190), konik kesitler çalışmasında önemli ilerlemeler kaydetti ve üç çeşit konik kesitin de, çift katlı bir koniyi kesen düzlemin açısını değiştirerek elde edilebileceğini gösterdi.[67] Ayrıca bugün konik kesitler için kullanılan terminolojiyi de icat etti, yani parabol ("yandaki yer, İngilizce: place beside" veya "karşılaştırma, İngilizce: comparison"), elips ("eksiklik, İngilizce: deficiency") ve hiperbol ("öteye atma, İngilizce: a throw beyond") terimleri kendisine aittir.[68] Konikler (İngilizce: Conics) çalışması, antik çağlardan kalma en iyi bilinen ve korunan matematiksel çalışmalardan biridir ve bu eserde Apollonius, konik bölümlerle ilgili Isaac Newton gibi gezegen hareketini inceleyen sonraki matematikçiler ve gökbilimciler için paha biçilmez olduğu kanıtlanacak birçok teorem türetmiştir.[69] Ne Apollonius ne de başka herhangi bir Yunan matematikçi, koordinat geometride atılım yapmamış olsa da, Apollonius'un eğrileri ele alması bazı yönlerden modern işleyişe benziyor ve çalışmalarının bir kısmı, yaklaşık 1800 yıl sonra Descartes tarafından analitik geometrinin gelişimi için ilham olmuş gibi görünüyor.[70]
Aynı zamanlarda, Cyreneli Eratosthenes (MÖ 276–194) asal sayıları bulmak için Eratosthenes Kalburunu tasarladı.[71] MÖ 3. yüzyıl, genel olarak Yunan matematiğinin "Altın Çağı" olarak kabul edilir ve bundan böyle saf matematikteki ilerlemeler göreli olarak azalır.[72] Bununla birlikte, takip eden yüzyıllarda uygulamalı matematikte, en önemlisi trigonometride, büyük ölçüde gökbilimcilerin ihtiyaçlarını karşılamak için önemli ilerlemeler kaydedildi.[72] Nicaealı Hipparchus (y. MÖ 190-120), bilinen ilk trigonometrik tabloyu derleyerek trigonometrinin kurucusu olarak kabul edilir ve 360 derecelik dairenin sistematik kullanımının kaynağı da kendisidir.[73] İskenderiyeli Heron (y. MS 10-70), bir skalen (eşkenar olmayan) üçgenin alanını bulmak için geliştirdiği Heron formülü ve negatif sayıların karekökleri olasılığını ilk fark eden kişi olarak anılır.[74] İskenderiyeli Menelaus (MS 100 dolayları) Menelaus teoremi aracılığıyla küresel trigonometriye öncülük etti.[75] Antik çağın en eksiksiz ve etkili trigonometrik çalışması, trigonometrik tabloları önümüzdeki bin yıl boyunca gökbilimciler tarafından kullanılacak ve astronomi için dönüm noktası sayılabilecek bir bilimsel çalışma olan Batlamyus'un Almagest'idir (y. MS 90-168).[76] Batlamyus ayrıca, trigonometrik büyüklükleri türetmek için Batlamyus teoremi ve orta çağ dönemine kadar Çin dışındaki en doğru π değeri olan 3,1416 ile de anılmaktadır.[77]

Batlamyus sonrası bir durgunluk döneminin ardından, MS 250 ve 350 arasındaki dönem, bazen Yunan matematiğinin "Gümüş Çağı" olarak anılır.[78] Bu dönemde Diophantus, cebirde, özellikle "Diophantine analizi" olarak da bilinen belirsiz analizde önemli ilerlemeler kaydetti.[79] Diophantine denklemleri ve Diophantine yaklaşımlarının incelenmesi bu güne kadar önemli bir araştırma alanıdır. Ana çalışması, belirli ve belirsiz denklemlerin kesin çözümleriyle ilgilenen 150 cebirsel problemden oluşan bir koleksiyon olan Arithmetica idi.[80] Arithmetica adlı eserin, eserde okuduğu bir problemi (kareyi iki kareye bölme problemi) genelleştirmeye çalıştıktan sonra ünlü "Son Teoremi"ne ulaşan Pierre de Fermat gibi sonraki matematikçiler üzerinde önemli bir etkisi oldu.[81] Diophantus ayrıca notasyonda önemli ilerlemeler kaydetti, Arithmetica cebirsel sembolizm ve senkopun ilk örneğiydi.[80]

Son büyük Yunan matematikçiler arasında İskenderiyeli Pappus (MS 4. yüzyıl) vardır. Altıgen teoremi ve ağırlık merkezi teoreminin yanı sıra Pappus konfigürasyonu ve Pappus grafı ile tanınır. Koleksiyon (İngilizce: Collection) adlı eserinin çoğu günümüze ulaştığı için, Yunan matematiği üzerine önemli bir bilgi kaynağıdır.[82] Pappus, Yunan matematiğinin son büyük yenilikçisi olarak kabul edilir ve sonraki çalışmaları çoğunlukla önceki çalışmalara ilişkin yorumlardan oluşur.

Tarih tarafından kaydedilen ilk kadın matematikçi İskenderiyeli Hypatia'ydı (MS 350-415). Büyük Kütüphanede Kütüphaneci olarak babasının (İskenderiyeli Theon) yerini aldı[84] ve uygulamalı matematik üzerine birçok çalışma yazdı. Siyasi bir anlaşmazlık nedeniyle, İskenderiye'deki Hristiyan cemaati onu halka açık bir şekilde soydu ve idam etti.[85] Proclus, Simplicius ve Eutocius gibi şahsiyetlerle başka bir yüzyıl boyunca Atina'da matematik çalışmaları devam etmesine rağmen, onun ölümü bazen İskenderiye Yunan matematiğinin sonu olarak alınır.[86] Proclus ve Simplicius, matematikçiden daha çok filozof olmalarına rağmen, önceki çalışmalar üzerine yaptıkları yorumlar Yunan matematiği üzerine değerli kaynaklardır. Neo-Platonik Atina Akademisi'nin MS 529'da imparator Justinian tarafından kapatılması, geleneksel olarak Yunan matematiğinin sonunun işareti olarak kabul edilir, ancak Yunan geleneği Bizans imparatorluğunda Ayasofya'nın mimarı olan Trallesli Anthemius ve Miletli Isidore gibi matematikçilerle kesintisiz devam etti.[87] Bununla birlikte, Bizans matematiği, çok az yenilikle çoğunlukla yorumlardan oluşuyordu ve bu dönemde matematiksel yeniliğin merkezleri başka yerlerde bulunacaktı.[88]
Roma

Etnik Yunan matematikçiler, geç Roma Cumhuriyeti ve sonraki Roma İmparatorluğu'nun yönetimi altında devam etseler de, diğerleriyle karşılaştırıldığında dikkate değer yerli Latin matematikçileri yoktu.[89][90] Yunanistan'da matematik okuyan etkili bir Roma devlet adamı olan Cicero (MÖ 106-43) gibi antik Romalılar, Romalı araştırmacıların ve hesap yapıcıların Yunanlar tarafından ödüllendirilen teorik matematik ve geometri yerine uygulamalı matematikle çok daha fazla ilgilendiğine inanıyorlardı.[91] Romalıların sayısal sistemlerini ilk önce doğrudan Yunan emsallerinden mi yoksa merkezi şu anda orta İtalya'da yer alan Toskana'da olan Etrüsk uygarlığınca kullanılan Etrüsk rakamlarından mı türettikleri açık değildir.[92]

Romalılar hesaplamayı kullanarak hem mali dolandırıcılığı teşvik etme hem de tespit etme ve ayrıca hazine için vergileri yönetme konusunda ustaydılar.[93] Romalı gromatikçilerden (yani arazi araştırmacısı) biri olan Siculus Flaccus, Romalı araştırmacılara tahsis edilmiş toprakların ve bölgelerin yüzey alanlarını ölçmede yardımcı olan Alanların Kategorileri (İngilizce: Categories of Fields) 'ni yazdı.[94] Romalılar, ticaret ve vergileri yönetmenin yanı sıra, köprüler, yol yapımı ve askeri mücadeleler için hazırlık gibi mimarinin kurulması da dahil olmak üzere mühendislikteki problemleri çözmek için düzenli olarak matematik uyguladılar.[95] Önceki Yunan tasarımlarından esinlenen Roma mozaikleri gibi sanat ve zanaat, illüzyonist geometrik desenler ve her biri ortalama sekiz milimetre karelik opus tessellatum parçaları ve ortalama dört milimetre kare yüzeye sahip daha ince opus vermiculatum parçalarından oluşan tessera karosu için hassas ölçümler gerektiren zengin ve ayrıntılı sahneler yarattılar.[96][97]
Roma takviminin oluşturulması da temel matematiği gerektiriyordu. İlk takvimin, Roma Krallığı döneminde MÖ 8. yüzyıla dayandığı ve her iki yılda bir 356 gün artı bir artık yılı içerdiği iddia ediliyor.[98] Buna karşılık, Cumhuriyet döneminin ay takvimi, güneş yılına göre kabaca on dört gün daha kısa olan 355 gün içeriyordu ve bu tutarsızlık 23 Şubat'tan sonra takvime fazladan bir ay eklenmesiyle çözüldü.[99] Bu takvimin yerini Jülyus Caesar (MÖ 100-44) tarafından düzenlenen ve İskenderiyeli Sosigenes tarafından 365 günlük bir döngüye dört yılda bir artık günü dahil edecek şekilde tasarlanan bir güneş takvimi olan Jülyen takvimi almıştır.[100] 11 dakika 14 saniyelik bir hata içeren bu takvim daha sonra, modern zamanlarda uluslararası standart takvimle neredeyse aynı güneş takvimi olan Papa XIII (1572-1585) tarafından düzenlenen Gregoryen takvimi ile düzeltildi.[101]
Aşağı yukarı aynı zamanlarda, Han Çinlileri ve Romalılar, gidilen mesafeleri ölçmek için tekerlekli kilometre sayacı cihazını icat ettiler. Roma modeli ilk kez Romalı inşaat mühendisi ve mimar Vitruvius tarafından tanımlandı (MÖ 80 - 15).[102] Cihaz en azından İmparator Commodus (MS 177 - 192) dönemine kadar kullanıldı, ancak tasarımı 15. yüzyılda Batı Avrupa'da deneyler yapılana kadar kaybolmuş görünüyor.[103] Belki de Antikythera mekanizmasında bulunan benzer teçhizat ve teknolojiye dayanarak, Vitruvius'un kilometre sayacı, bir Roma milinde (kabaca 4590 ft / 1400 m) dört yüz kez dönen, çapı 4 feet (1,2 m) olan araba tekerleklerine sahipti. Her devirde, bir pim ve aks, çakılları bir kutuya düşürmekten sorumlu ikinci bir dişliyi çeviren 400 dişli bir çarkı devreye aldı, her bir çakıl taşı bir mil katetmeyi temsil ediyordu.[104]
Çin

Erken Çin matematiğinin analizi sonucu dünyanın diğer bölgelerine kıyasla eşsiz bir gelişim gösterdiği anlaşıldığından bilim adamları Çin matematiğinin tamamen bağımsız bir gelişimi olduğunu varsaymaya yöneltti.[105] Çin'den günümüze ulaşan en eski matematiksel metin, MÖ 1200 ile MÖ 100 arasına tarihlenen Zhoubi Suanjing'dir, ancak Savaşan Devletler Çağı'nda y. MÖ 300 tarihi makul görünmektedir.[106] Bilinen en eski ondalık çarpım tablosunu içeren Tsinghua Bambu Fişleri (her ne kadar eski Babilliler 60'lık bir tabana sahip olsa da) ise MÖ 305 civarına tarihlenmektedir ve belki de Çin'in hayatta kalan en eski matematiksel metnidir.[45]
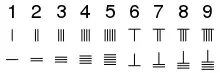

Çin matematiğinde 1 ile 10 arasındaki sayılar için farklı anahtarların kullanıldığı "çubuk rakamları" ve on'un kuvvetleri için ek anahtarların kullanıldığı ondalık konumsal notasyon sisteminin Çin matematiğinde kullanılması özellikle dikkat çekicidir.[107] Böylece, 123 sayısı "1" simgesi, ardından "100" simgesi, ardından "2" simgesi ve ardından "10" simgesi ve ardından "3" simgesi kullanılarak yazılacaktır. Bu, o zamanlar dünyadaki en gelişmiş sayı sistemiydi, görünüşe göre ortak çağdan birkaç yüzyıl önce ve Hint rakam sisteminin geliştirilmesinden çok önce kullanılıyordu.[108] Çubuk rakamları, sayıların istenildiği kadar büyük gösterilmesine ve hesaplamaların "suan pan" veya Çin abaküsünde yapılmasına izin verdi. Suan pan'ın icat tarihi kesin olmamakla birlikte, Xu Yue'nin Şekillerin Sanatı Üzerine Ek Notlar (İngilizce: Supplementary Notes on the Art of Figures) 'ında hakkındaki ilk yazılı sözler MS 190'dan kalmadır.
Çin'de geometri üzerine var olan en eski çalışma felsefi Mohist kanondan, y. MÖ 330'den gelmekte olup Mozi'nin (MÖ 470–390) takipçileri tarafından derlenmiştir. Mo Jing, fizik bilimi ile ilgili birçok alanın çeşitli yönlerini tanımladı ve az sayıda geometrik teorem de buldu.[109] Aynı zamanda çevre, çap, yarıçap ve hacim kavramlarını da tanımladı.[110]

MÖ 212'de, İmparator Qin Shi Huang, Qin İmparatorluğu'nda resmi olarak onaylanmış olanlar dışındaki tüm kitapların yakılmasını emretti. Bu kararnameye evrensel olarak uyulmadı, ancak bu düzenin bir sonucu olarak, bu tarihten önce eski Çin matematiği hakkında çok az şey biliniyor. MÖ 212 yılındaki kitapların yakılmasından sonra Han hanedanı (MÖ 202 - MS 220) muhtemelen şu anda kaybolan eserler üzerine genişletilmiş matematik eserleri üretti. Bunlardan en önemlisi, tam adı MS 179'da ortaya çıkan, ancak daha önce başka başlıklar altında kısmen var olan Matematik Sanatına İlişkin Dokuz Bölüm (İngilizce: The Nine Chapters on the Mathematical Art) 'dür. Tarım, iş, Çin pagoda kuleleri için yükseklik aralıklarını ve boyut oranlarını belirlemek için geometri kullanımı, mühendislik, ölçme ve dik üçgenler üzerine maddeler içeren 246 kelime probleminden oluşur.[106] Pisagor teoremi için matematiksel bir kanıt[111] ve Gauss yok etme yöntemi için matematiksel bir formül yarattı.[112] Bilimsel çalışma ayrıca, Liu Xin (ö. MS 23) 3,1457 değerini sağlayana kadar ve ardından Zhang Heng (MS 78-139) π'yi 3,1724[113] olarak yaklaşık olarak verene kadar Çinli matematikçilerin başlangıçta 3 olarak yaklaştıkları π değerlerini[106] ve 10'un karekökünü alarak 3,162 değerini[114][115] sağlar. Liu Hui, MS 3. yüzyılda Dokuz Bölüm hakkında yorum yaptı ve 5 ondalık basamağa kadar doğru π değerini verdi (yani 3,14159).[116][117] Teorik anlayıştan çok bir hesaplama dayanıklılığı meselesi olsa da, MS 5. yüzyılda Zu Chongzhi, π'nin yedi ondalık basamağının değerini (yani, 3,141592) hesapladı ve bu, neredeyse sonraki 1000 yıl boyunca en doğru π değeri olarak kaldı.[116][118] Ayrıca bir kürenin hacmini bulmak için, daha sonra Cavalieri prensibi olarak anılacak bir yöntem geliştirdi.[119]
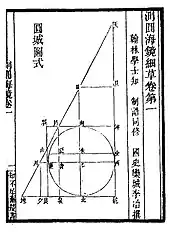
Çin matematiğinin doruk noktası, 13. yüzyılda Song hanedanlığının ikinci yarısında (MS 960-1279) Çin cebirinin gelişmesiyle ortaya çıktı. Bu dönemin en önemli metni Zhu Shijie'nin (1249-1314) Dört Elementin Değerli Aynası (İngilizce: Precious Mirror of the Four Elements) 'dır ve Horner yöntemine benzer bir yöntem kullanarak eşzamanlı yüksek dereceden cebirsel denklemlerin çözümünü ele alır.[116] Değerli Ayna, aynı zamanda, her ikisi de 1100 gibi erken bir tarihte Çin eserlerinde görünse de, sekizinci kuvvet yoluyla iki terimli genişleme katsayılarıyla birlikte Pascal üçgeninin bir diyagramını da içerir.[121] Çinliler ayrıca eski zamanlarda tanımlanan ve Yang Hui (MS 1238-1298) tarafından mükemmelleştirilen sihirli kare ve sihirli daireler olarak bilinen karmaşık kombinatoryal diyagramdan da yararlandı.[121]
Avrupa matematiği Rönesans sırasında gelişmeye başladıktan sonra bile, Avrupa ve Çin matematiği ayrı geleneklerdi ve 13. yüzyıldan itibaren önemli Çin matematiksel çıktıları geriledi. Matteo Ricci gibi Cizvit misyonerler, 16. yüzyıldan 18. yüzyıla kadar matematiksel fikirleri iki kültür arasında ileri geri taşıdılar, ancak bu noktada Çin'den yayılmaktan çok daha fazla matematiksel fikir Çin'e giriyordu.[121]
Japon matematiği, Kore matematiği ve Vietnam matematiği geleneksel olarak Çin matematiğinden kaynaklanmaktadır ve Konfüçyüsçü temelli Doğu Asya kültür alanına ait olarak görülmektedir.[122] Kore ve Japon matematiği, Çin'in Song hanedanlığı döneminde üretilen cebirsel çalışmalardan büyük ölçüde etkilenirken, Vietnam matematiği, Çin'in Ming hanedanlığının (1368-1644) popüler eserlerine büyük ölçüde borçludur.[123] Örneğin, Vietnam matematiksel incelemeleri ya Çince ya da yerli Vietnamca Chữ Nôm alfabesiyle yazılmış olsa da, bunların tümü, bunları çözmek için algoritmalar içeren bir problemler koleksiyonunu sunan Çin formatını ve ardından sayısal cevapları izledi.[124] Vietnam ve Kore'de matematik çoğunlukla matematikçiler ve astronomların profesyonel mahkeme bürokrasisiyle ilişkilendirilirken, Japonya'da özel okullar alanında daha yaygındı.[125]
Hint


Hint yarımadasındaki en eski uygarlık, İndus nehri havzasında gelişen İndus Vadisi Uygarlığı'dır (olgunluk dönemi: MÖ 2600-1900). Şehirleri geometrik düzende düzenlenmiştir, ancak bu uygarlıktan bilinen hiçbir matematiksel belge günümüze kalmamıştır.[127]
Hindistan'dan günümüze ulaşan en eski matematiksel kayıtlar, Sulba Sutralarıdır (MÖ 8. yüzyıl ile MS 2. yüzyıl arasında çeşitli tarihlere tarihlenmiştir.)[128], kare, dikdörtgen, paralel kenarlar ve diğerleri gibi çeşitli şekillerde[129] sunaklar inşa etmek için basit kurallar veren dini metinlere ek bölümlerdir. Mısır'da olduğu gibi, tapınak işlevlerine ilişkin meşguliyet, matematiğin dinsel ritüeldeki kökenine işaret etmektedir.[128] Sulba Sutraları, belirli bir kare ile yaklaşık olarak aynı alana sahip bir çember oluşturmak için yöntemler verir, bu da π değerinin birkaç farklı yaklaşımını ifade eder.[130][131][lower-alpha 1] Ek olarak, 2 ila birkaç ondalık basamağın karekökünü hesaplar, Pisagor üçlülerini listeler ve Pisagor teoreminin bir açıklamasını verirler.[131] Tüm bu sonuçlar, Mezopotamya etkisini gösteren Babil matematiğinde mevcuttur.[128] Sulba Sutralarının daha sonraki Hint matematikçileri ne ölçüde etkilediği bilinmemektedir. Çin'de olduğu gibi Hint matematiğinde de süreklilik sorunu vardır; önemli ilerlemeler uzun hareketsizlik dönemleri ile tarihsel olarak birbirinden ayrılır.[128]
Pāṇini (MÖ 5. yüzyıl) Sanskrit dil bilgisi kurallarını formüle etti.[132] Onun notasyonu, modern matematiksel gösterime benziyordu ve üst kurallar, dönüşümler ve özyineleme kullandı.[133] Pingala (kabaca MÖ 3. – 1. yüzyıllar), aruz üzerine yaptığı incelemede ikili sayı sistemine karşılık gelen bir cihaz kullanır.[134][135] Sayaçların kombinasyonlarıyla ilgili tartışması, binom teoreminin basit bir versiyonuna karşılık gelir. Pingala'nın çalışması aynı zamanda Fibonacci sayılarının (mātrāmeru olarak adlandırılır) temel fikirlerini de içerir.[136]
Sulba Sutralarından sonra Hindistan'dan gelen bir sonraki önemli matematiksel belge, güçlü Helenistik etkiler görülen ve MS 4. ve 5. yüzyıllara (Gupta dönemi) tarihlenen astronomik incelemeler olan Siddhantas'tır.[137] Ptolemaik trigonometride olduğu gibi tam kiriş yerine modern trigonometride olduğu gibi yarı kirişe dayalı trigonometrik ilişkilerin ilk örneğini içermeleri bakımından önemlidirler.[138] Bir dizi çeviri hatası aracılığıyla, "sinüs" ve "kosinüs" kelimeleri Sanskritçe "jiya" ve "kojiya" dan türemiştir.[138]
MS 500 civarında, Aryabhata, mantık veya tümdengelimli metodoloji duygusu olmaksızın, astronomi ve matematiksel ölçmede kullanılan hesaplama kurallarını tamamlamayı amaçlayan, nazım biçiminde yazılmış ince bir cilt olan Aryabhatiya'yı yazdı.[139] Kayıtların yaklaşık yarısı yanlış olsa da, Aryabhatiya'da ilk olarak ondalık basamak-değer sisteminin ortaya çıktığı görülmektedir. Birkaç yüzyıl sonra Müslüman matematikçi Ebu Rayhan Biruni, Aryabhatiya'yı "sıradan çakıl taşları ve pahalı kristallerin bir karışımı" olarak tanımladı.[140]
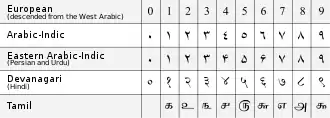
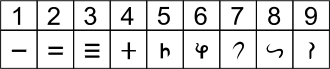
7. yüzyılda Brahmagupta, Brahmagupta teoremini, Brahmagupta özdeşliğini ve Brahmagupta formülünü tanımladı ve ilk kez Brahma-sphuta-siddhanta 'da sıfırın hem yer tutucu hem de ondalık basamak olarak açıkça kullanımını ve Hint–Arap rakam sistemini açıkladı.[141] Matematik üzerine yazılmış bu Hint metninin çevirisinden (y. 770), İslami matematikçiler Arap rakamları olarak uyarladıkları sayı sistemini tanıttı. İslam alimleri, bu sayı sistemi bilgisini 12. yüzyılda Avrupa'ya taşıdı ve şimdi tüm dünyadaki eski sayı sistemlerinin yerini aldı. Hint-Arap sayı sistemindeki sayıları temsil etmek için çeşitli simge kümeleri kullanılır ve bunların tümü Brahmi sayılarından geliştirilmiştir. Hindistan'ın kabaca düzinelerce önemli el yazısının her birinin kendi sayısal kabartmaları vardır. 10. yüzyılda, Halayudha'nın Pingala'nın çalışması üzerine yaptığı yorum, Fibonacci dizisi ve Pascal üçgeni ile ilgili çalışmaları içerir ve bir matrisin oluşumunu tanımlar.[142]
12. yüzyılda, Bhāskara II[143] güney Hindistan'da yaşadı ve o zamanlar bilinen tüm matematik dalları üzerine kapsamlı bir şekilde yazdı. Çalışması, sonsuz küçüklere eşdeğer veya yaklaşık olarak eşdeğer matematiksel nesneler, türevler, ortalama değer teoremi ve sinüs fonksiyonunun türevini içerir. Analizin icadının matematik tarihçileri arasında ne ölçüde tartışmalı bir konu olduğunu tahmin etti.[144]
14. yüzyılda, Kerala Matematik Okulu'nun kurucusu olan Sangamagramalı Madhava, Madhava-Leibniz serisini buldu ve ondan faydalanarak π'nin ilk 21 basamak değerini 3,14159265359 olarak hesaplayan dönüştürülmüş bir seri elde etti. Madhava ayrıca arktanjantı belirlemek için Madhava-Gregory serisini, sinüs ve kosinüsü belirlemek için Madhava-Newton kuvvet serisini, sinüs ve kosinüs fonksiyonları için Taylor yaklaşımını buldu.[145] 16. yüzyılda Jyesthadeva, Kerala Okulu'nun Yukti-bhāṣā’daki gelişmelerinin ve teoremlerinin çoğunu birleştirdi.[146] [147] Analizin temellerini atan Kerala Okulunun ilerlemelerinin 16. yüzyılda Avrupa'ya aktarıldığı ileri sürülmüştür.[148] Cizvit misyonerler ve tüccarlar aracılığıyla o zamanlar antik Muziris limanı çevresinde faaliyet gösterdiler ve sonuç olarak, analiz ve hesaplamadaki sonraki Avrupa gelişmelerini doğrudan etkilediler.[149] Bununla birlikte, diğer bilim adamları Kerala Okulu'nun sistematik bir türev ve integral teorisi formüle etmediğini ve sonuçlarının Kerala dışına iletildiğine dair doğrudan kanıtlar olmadığını savunuyorlar.[150][151][152][153]
İslam
8. yüzyılda İran, Orta Doğu, Orta Asya, Kuzey Afrika, İberya ve Hindistan'ın bazı bölgelerinde kurulan İslam İmparatorluğu, matematiğe önemli katkılarda bulundu. Matematikle ilgili İslami metinlerin çoğu Arapça yazılmış olsa da, çoğu Araplar tarafından yazılmamıştır, çünkü Yunancanın Helenistik dünyadaki durumuna çok benzer şekilde Arapça da o zaman İslam dünyasında Arap olmayan bilginlerin yazı dili olarak kullanılmıştır. Arapların yanı sıra Persler de Matematik dünyasına katkıda bulundular.
9. yüzyılda, İranlı matematikçi Ebû Ca'fer Muhammed bin Mûsâ el-Hârizmî, Hint-Arap rakamları ve denklem çözme yöntemleri üzerine birkaç önemli kitap yazdı. El-Kindi'nin çalışmaları ile birlikte yaklaşık 825'te yazdığı Hint rakamları ile hesap üzerine (İngilizce: On the Calculation with Hindu Numerals) adlı kitabı Hint matematiğinin ve Hint rakamlarının Batı'ya yayılmasında etkili oldu. Algoritma kelimesi, isminin Latinleştirilmesi olan Algoritmi'den ve cebir kelimesi de eserlerinden biri olan Cebir ve Denklem Hesabı Üzerine Özet Kitap (Arapça: El'Kitab'ül-Muhtasar fi Hısab'il Cebri ve'l-Mukabele, İngilizce: The Compendious Book on Calculation by Completion and Balancing) adlı eserinden türetilmiştir. Pozitif köklü ikinci dereceden denklemlerin cebirsel çözümü için kapsamlı bir açıklama yaptı [154] ve cebiri temel formda ve sadece cebrin kendisi için (dolaylı fayda ve beklentilerden arınmış olarak) öğreten ilk kişi oldu.[155] Ayrıca, çıkarılmış terimlerin bir denklemin diğer tarafına aktarılmasına, yani denklemin zıt taraflarında benzer terimlerin iptaline atıfta bulunarak "indirgeme" ve "dengeleme" nin temel yöntemini tartıştı. Bu Harezmi'nin başlangıçta "el-Cebr" olarak tanımladığı işlemdir.[156] Onun cebiri artık "çözülmesi gereken bir dizi problemle değil, kombinasyonların denklemler için olası tüm prototipleri vermesi gereken ilkel terimlerle başlayan ve bundan böyle açıkça çalışmanın gerçek amacını oluşturan bir açıklama" ile ilgileniyordu. Ayrıca sadece kendi iyiliği için bir denklem üzerinde çalıştı ve "genel bir şekilde, basitçe bir problem çözme sırasında ortaya çıkmasa bile, ancak özellikle problem sınıflarını belirli ve sonsuz olarak adlandırmıştır."[157]
Mısır'da Ebu Kamil, cebri irrasyonel sayılar kümesine genişletti, karekökleri ve dördüncü kökleri ikinci dereceden denklemlere çözümler ve katsayılar olarak kabul etti. Ayrıca, üç bilinmeyen değişkenli, üç doğrusal olmayan eşzamanlı denklemi çözmek için kullanılan teknikleri geliştirdi. Çalışmalarının benzersiz bir özelliği, 2676 çözüm bulduğu bir tanesi de dahil olmak üzere, bazı problemlerin olası tüm çözümlerini bulmaya çalışmaktı.[158] Eserleri cebirin gelişimi için önemli bir temel oluşturdu ve El-Kereci ve Fibonacci gibi daha sonraki matematikçileri etkiledi.
Cebirdeki diğer gelişmeler, El-Kereci tarafından, metodolojiyi bilinmeyen büyüklüklerin tam sayı güçlerini ve tam sayı köklerini içerecek şekilde genişlettiği al-Fakhri incelemesinde yapılmıştır. Matematiksel tümevarımla ispata yakın bir çalışma, El-Kereci tarafından MS 1000 civarında yazılan ve onun Binom teoremini, Pascal üçgenini ve integral küplerin toplamını kanıtlamak için kullandığı bir kitapta ortaya çıkmıştır.[160] Matematik tarihçisi F. Woepcke[161], El-Kereci'yi "cebirsel hesap teorisini ortaya atan ilk kişi" olarak övdü. Ayrıca 10. yüzyılda Ebu Vefa, Diophantus'un eserlerini Arapçaya çevirdi. İbn-i Heysem, herhangi bir integral kuvvetin toplamının genel formülünü belirlemek için kolayca genelleştirilebilen bir yöntem kullanarak dördüncü kuvvetlerin toplamı için formül türeten ilk matematikçiydi. Bir paraboloidin hacmini bulmak için bir integral hesabı gerçekleştirdi ve sonucunu dördüncü dereceye kadar polinomların integralleri için genelleştirebildi. Böylece, polinomların integralleri için genel bir formül bulmaya yaklaştı, ancak dördüncü dereceden daha yüksek herhangi bir polinomla ilgilenmedi.[162]
11. yüzyılın sonlarında, Ömer Hayyam, Öklid'in Elemanları (İngilizce: Elements) 'nda, özellikle de paralellik postülatında kusurlar olarak algıladığı şeyler hakkında bir kitap olan Öklid'deki Zorlukların Tartışmaları İngilizce: Discussions of the Difficulties in Euclid 'nı yazdı. Ayrıca kübik denklemlerin genel geometrik çözümünü bulan ilk kişi oydu. Takvim reformunda da çok etkili oldu.[163]
13. yüzyılda Nasîrüddin Tûsî küresel trigonometride ilerleme kaydetti. Ayrıca Öklid'in paralellik postülatı üzerine etkili çalışmalar yazdı. 15. yüzyılda, Gıyaseddin El-Kaşi, π'nin değerini 16. ondalık basamağa kadar doğru hesapladı. Kaşi ayrıca, yüzyıllar sonra Ruffini ve Horner tarafından verilen yöntemlerin özel bir durumu olan n'inci kökleri hesaplamak için bir algoritmaya sahipti.
Müslüman matematikçilerin bu dönemdeki diğer başarıları arasında Arap rakamlarına ondalık nokta notasyonunun eklenmesi, sinüsün yanı sıra tüm modern trigonometrik fonksiyonların keşfi, el-Kindi'nin kriptanaliz ve frekans analizi ile ilgili çalışmaları, İbn-Heysem tarafından analitik geometrinin gelişimi, Ömer Hayyam tarafından cebirsel geometrinin başlangıcı ve El-Kalsâdî tarafından cebirsel bir notasyonun geliştirilmesi vardır.[164]
15. yüzyıldan itibaren Osmanlı İmparatorluğu ve Safevi İmparatorluğu döneminde İslam matematiğinin gelişimi durağanlaştı.
Maya
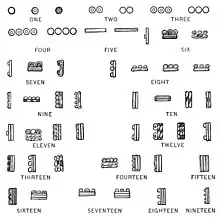
Kolomb Öncesi Amerika'da, MS 1. binyılda Meksika ve Orta Amerika'da gelişen Maya uygarlığı, coğrafi izolasyonu nedeniyle mevcut Avrupa, Mısır ve Asya matematiklerinden tamamen bağımsız olan benzersiz bir matematik geleneği geliştirdi.[165] Maya rakamları, çoğu modern kültür tarafından kullanılan ondalık sistemin temelini oluşturan onluk bir taban yerine, vigesimal sistem olan 20 tabanını kullandı.[165] Mayalar, Maya takvimini oluşturmak için matematiği kullandılar ve kendi doğal Maya astronomilerindeki astronomik olayları tahmin ettiler.[165] Pek çok çağdaş kültürün matematiğine sıfır kavramı girmek zorunda kalınca, Mayalar bunun için standart bir sembol geliştirdiler.[165]
Ortaçağ Avrupası
Orta Çağ Avrupası'nın matematiğe ilgisi, modern matematikçilerinkinden oldukça farklı kaygılardan kaynaklanıyordu. İtici unsurlardan biri, matematiğin, yaratılan doğa düzenini anlamanın anahtarı olduğu inancıydı. Bu düşünce, sıklıkla Platon'un Timaeus 'u ve İncil pasajında (Bilgelik Kitabı-Book of Wisdom-'nda) "Tanrı her şeyi ölçü, sayı ve ağırlık olarak buyurmuştur" ifadesine dayandırıldı.[166]
Boethius, aritmetik, geometri, astronomi ve müzik çalışmalarını tanımlamak için quadrivium terimini icat ettiğinde 6. yüzyılda müfredatta matematik için bir yer sağladı. Nicomachus'un Yunanca Aritmetiğe Giriş İngilizce: Introduction to Arithmetic 'inden özgür bir çeviri olan De Institute arithmetica 'yı yazdı. Ayrıca De corpore musica, Yunan kaynaklarından türetilmiştir. Öklid'in Elemanlar 'ından bir dizi alıntı yapmıştır. Çalışmaları pratik olmaktan çok teorikti ve Yunanca ve Arapça matematik çalışmalarının iyileşmesine kadar matematiksel çalışmanın temelini oluşturdu.[167][168]
12. yüzyılda, Avrupalı akademisyenler, El-Harizmi'nin, Chester'li Robert tarafından Latince'ye çevrilen Cebir ve Denklem Hesabı Üzerine Özet Kitap (Arapça: El'Kitab'ül-Muhtasar fi Hısab'il Cebri ve'l-Mukabele, İngilizce: The Compendious Book on Calculation by Completion and Balancing) adlı eserini ve Bath'li Adelard, Carinthia'lı Herman ve Cremonalı Gerard tarafından çevrilen Öklid'in Elemanlar 'ının tam metni dahil olmak üzere bilimsel Arapça metinler aramak için İspanya ve Sicilya'ya gittiler.[169][170] Bunlar ve diğer yeni kaynaklar matematiğin yenilenmesini ateşledi.
Şimdi Fibonacci olarak bilinen Pisa'lı Leonardo, tüccar babasıyla şimdiki Cezayir'in Béjaïa kentine yaptığı bir yolculukta Hint-Arap rakamlarını tesadüfen öğrendi. (Avrupa o zaman hala Roma rakamlarını kullanıyordu.) Orada, Hint-Arap rakamlarının konumsal gösterimi nedeniyle çok daha verimli olan ve ticareti büyük ölçüde kolaylaştıran bir aritmetik sistemini (özellikle algorism - Arap rakamları sistemi) gözlemledi. Leonardo, 1202'de Liber Abaci 'yi yazarak (1254'te güncellendi) tekniği Avrupa'ya tanıttı ve onu popülerleştirmek için uzun bir dönem başlattı. Kitap ayrıca Avrupa'ya, metinde dikkate değer olmayan bir örnek olarak kullanılan ve şimdi Fibonacci dizisi olarak bilinen (bundan önce yüzlerce yıldır Hint matematikçiler tarafından biliniyordu) diziyi tanıttı.
14. yüzyıl, çok çeşitli problemleri araştırmak için yeni matematiksel kavramların geliştirilmesine tanık oldu.[171] Önemli bir katkı da yerel hareket (local motion) matematiğinin gelişmesiydi.
Thomas Bradwardine, kuvvetin (F), dirence (R) oranı geometrik oranda arttıkça hızın (V) aritmetik oranda arttığını öne sürdü. Bradwardine bunu bir dizi özel örnekle ifade etti, ancak logaritma henüz tasarlanmamış olmasına rağmen, sonucunu içinde bulunulan döneme uygun düşmeyen bir biçimde şöyle yazarak ifade edebiliriz: V = log (F / R).[172] Bradwardine'in analizi, el-Kindi ve Villanova'lı Arnald tarafından bileşik ilaçların doğasını farklı bir fiziksel problemle ölçmek için kullanılan matematiksel bir tekniğin aktarılmasına bir örnektir.[173]

14. yüzyıl Oxford Hesaplayıcılarından biri olan William Heytesbury, diferansiyel hesap ve limit kavramından yoksun, "bir cisim tarafından tanımlanan bir yol boyunda eğer ... o, aynı hızda düzgün olarak ve verilen anda hareket ederse" anlık hızı ölçmeyi önerdi.[175]
Heytesbury ve diğerleri, tekdüze hızlandırılmış harekete geçen bir cismin katettiği mesafeyi matematiksel olarak belirlediler (günümüzde integral ile çözüldü), "[hızı] eşit olarak artan veya azalan hareketli bir cisim, eğer ortalama [hız] derecesiyle aynı anda sürekli hareket ediyor olsaydı belirli bir zamanda tamamen eşit bir [mesafe] katedecekti".[176]
Paris Üniversitesi'nden Nicole Oresme ve İtalyan Giovanni di Casali, sabit ivmeyi gösteren çizginin altındaki alanın kat edilen toplam mesafeyi temsil ettiğini öne sürerek, bu ilişkinin grafiksel gösterimini bağımsız olarak sağladılar.[177] Öklid'in Elemanları üzerine daha sonraki bir matematiksel yorumda, Oresme, daha ayrıntılı bir genel analiz yaptı ve bu analizde, bir cismin her ardışık zaman artışında, tek sayılar olarak artan herhangi bir nitelikte bir artış elde edeceğini gösterdi. Öklid, tek sayıların toplamının kare sayılar olduğunu gösterdiği için, cismin kazandığı toplam nitelik zamanın karesi olarak artar.[178]
Rönesans
Rönesans döneminde matematiğin ve muhasebenin gelişimi iç içe geçmişti.[179] Cebir ve muhasebe arasında doğrudan bir ilişki bulunmamakla birlikte, konuların öğretimi ve yayınlanan kitaplar, genellikle ticaret ve alım-satım için yararlı becerileri öğrendikleri yer olan hesap okullarına (Flanders ve Almanya'da) veya abaküs okullarına (İtalya'da abbaco olarak bilinir) gönderilen tüccar çocuklarına yöneliktir. Defter tutma işlemlerini gerçekleştirirken muhtemelen cebire ihtiyaç yoktur, ancak karmaşık takas işlemleri veya bileşik faizin hesaplanması için temel bir aritmetik bilgisi zorunluydu ve cebir bilgisi çok faydalıydı.
Piero della Francesca (y. 1415-1492) uzay geometri ve doğrusal perspektif üzerine kitaplar yazdı, bunlara De Prospectiva Pingendi (Resim için Perspektif Üzerine, On Perspective for Painting), Trattato d'Abaco (Abaküs İncelemesi, Abacus Treatise) ve De corporibus regularibus (Düzgün Katılar, Regular Solids) dahildir.[180][181][182]

Luca Pacioli'nin İtalyanca: Summa de Arithmetica, Geometria, Proportioni et Proportionalità (İngilizce: Review of Arithmetic, Geometry, Ratio and Proportion, Türkçe: Aritmetik, Geometri, Oran ve Orantı İncelemesi) adlı eseri ilk olarak 1494'te Venedik'te basılmış ve yayınlanmıştır. Defter tutma üzerine 27 sayfalık bir inceleme içeriyordu, İtalyanca: Particularis de Computis et Scripturis (İngilizce: Details of Calculation and Recording, Türkçe: Hesaplama ve Kayıt Tutma Ayrıntıları). Öncelikle kitap bir referans metnidir, içerdiği matematiksel bulmacalardan bir zevk kaynağı olarak ve oğullarının eğitimine yardımcı olmak için kullanan tüccarlar için yazılmış, esas olarak satılmıştır.[183] Summa Arithmetica 'da Pacioli, artı ve eksi sembollerini ilk kez basılı bir kitapta tanıttı, semboller İtalyan Rönesans matematiğinde standart gösterim haline geldi. Summa Arithmetica aynı zamanda cebir içeren İtalya'da basılan ilk bilinen kitaptı. Pacioli fikirlerinin çoğunu intihal yaptığı Piero Della Francesca'dan aldı.
İtalya'da, 16. yüzyılın ilk yarısında, Scipione del Ferro ve Niccolò Fontana Tartaglia kübik denklemler için çözümler keşfetti. Gerolamo Cardano, bunları öğrencisi Lodovico Ferrari tarafından keşfedilen dördüncü derece denklemler için bir çözümle birlikte 1545 tarihli Ars Magna adlı kitabında yayınladı. 1572'de Rafael Bombelli, Cardano'nun kübik denklemleri çözme formülünde ortaya çıkabilecek hayali niceliklerle nasıl başa çıkılacağını gösterdiği L'Algebra kitabını yayınladı.
Simon Stevin'in ilk kez 1585'te Hollandaca yayınlanan De Thiende (İngilizce: the art of tenths, Türkçe: ondalıkların sanatı) adlı kitabı, ondalık gösterimin ilk sistematik işleyişini içeriyordu ve bu, daha sonra gerçek sayı sistemi üzerindeki tüm çalışmaları etkiledi.
Trigonometri, navigasyon gereksinimi ve geniş alanların doğru haritalarına duyulan artan ihtiyaç nedeniyle matematiğin önemli bir dalı haline geldi. Bu kelimeyi ilk kullanan Bartholomaeus Pitiscus, 1595'te Trigonometria 'sını yayınladı. Regiomontanus'un sinüs ve kosinüs tablosu 1533'te yayınlandı.[184]
Rönesans döneminde sanatçıların doğal dünyayı gerçekçi bir şekilde temsil etme arzusu, Yunanların yeniden keşfedilen felsefesiyle birlikte sanatçıları matematik çalışmaya yöneltti. Onlar aynı zamanda o zamanın mühendisleri ve mimarlarıydılar ve her halükarda matematiğe ihtiyaçları vardı. Perspektifte resim sanatı ve bununla ilgili geometrideki gelişmeler yoğun bir şekilde çalışıldı.[185]
Bilimsel Devrim Sırasında Matematik
17. yüzyıl
17. yüzyılda, Avrupa'da matematiksel ve bilimsel fikirlerde benzeri görülmemiş bir artış görüldü. Galileo, Hollanda'dan ithal edilen ve bir oyuncaktan esinlenen bir teleskop kullanarak Jüpiter'in uydularını bu gezegen çevresindeki yörüngede gözlemledi. Tycho Brahe, gökyüzündeki gezegenlerin konumlarını tanımlayan muazzam miktarda matematiksel veri toplamıştı. Johannes Kepler, Brahe'nin asistanı olarak pozisyonu sayesinde, gezegensel hareket konusuna ilk kez maruz kaldı ve ciddi bir şekilde etkileşime girdi. Kepler'in hesaplamaları, John Napier ve Jost Bürgi'nin çağdaş logaritma icadı ile daha basit hale getirildi. Kepler, gezegen hareketinin matematiksel yasalarını formüle etmeyi başardı.[186] René Descartes (1596–1650) tarafından geliştirilen analitik geometri, bu yörüngelerin Kartezyen koordinatlarda bir grafik üzerinde çizilmesine imkan verdi.
Birçok öncülünün daha önceki çalışmalarına dayanarak, Isaac Newton, Kepler'in Yasalarını açıklayan fizik yasalarını keşfetti ve şimdi kalkülüs olarak bilinen kavramları bir araya getirdi. 17. yüzyılın tartışmasız en önemli matematikçilerinden biri olan Gottfried Wilhelm Leibniz bağımsız olarak bugün hala kullanılmakta olan kalkülüs ve kalkülüs notasyonunu geliştirdi. Bilim ve matematik, yakında tüm dünyaya yayılacak olan uluslararası bir çaba haline geldi.[187]

Matematiğin göklerdeki çalışmalara uygulanmasının yanı sıra, Pierre de Fermat ve Blaise Pascal'ın yazışmaları ile uygulamalı matematik yeni alanlara doğru genişlemeye başlamıştır. Pascal ve Fermat, bir kumar oyunu üzerine tartışmalarında olasılık teorisi ve buna karşılık gelen kombinatorik kurallarının araştırılması için zemin hazırladı. Pascal, bahse girmesiyle, başarı olasılığı küçük olsa bile ödüllerin sonsuz olduğu gerekçesiyle, yeni gelişen olasılık teorisini dine adanmış bir yaşamı savunmak için kullanmaya çalıştı. Bu, bir anlamda, fayda teorisinin 18. – 19. yüzyıldaki gelişiminin habercisiydi.
18. yüzyıl

18. yüzyılın en etkili matematikçisi muhtemelen Leonhard Euler'di. Katkıları, Königsberg'in Yedi Köprüsü problemi ile graf teorisi çalışmasının kurulmasından, birçok modern matematiksel terim ve gösterimi standartlaştırmaya kadar uzanmaktadır. Örneğin, eksi 1'in karekökünü i sembolüyle adlandırdı ve bir dairenin çevresinin çapına oranını belirtmek için Yunanca harfinin kullanımını popüler hale getirdi. Topoloji, graf teorisi, kalkülüs, kombinatorik ve karmaşık analiz çalışmalarına, adını verdiği çok sayıda teorem ve notasyonla kanıtlandığı üzere çok sayıda katkı yaptı.
18. yüzyılın diğer önemli Avrupalı matematikçileri arasında sayı teorisi, cebir, diferansiyel hesap ve varyasyonlar hesabında öncü çalışmalar yapan Joseph Louis Lagrange ve Napolyon çağında gök mekaniğinin temelleri ve istatistik üzerine önemli çalışmalar yapan Laplace yer alıyor.
Modern
19. yüzyıl
19. yüzyıl boyunca matematik giderek daha soyut hale geldi. Carl Friedrich Gauss (1777–1855) bu eğilimi özetler. Bilime birçok katkısını bir kenara bırakarak, karmaşık değişkenlerin fonksiyonları, geometri ve serilerin yakınsaması üzerine devrim niteliğinde çalışmalar yaptı. Ayrıca, cebirin temel teoreminin ve ikinci dereceden karşılıklılık yasasının tatmin edici ilk kanıtlarını verdi.

Bu yüzyıl, Öklid geometrisinin paralellik postülatının artık geçerli olmadığı, Öklid dışı geometrinin iki formunun gelişimini gördü. Rus matematikçi Nikolai Ivanovich Lobachevsky ve rakibi Macar matematikçi János Bolyai, paralelliklerin benzersizliğinin artık geçerli olmadığı hiperbolik geometriyi bağımsız olarak tanımladı ve inceledi. Bu geometride, bir üçgendeki açıların toplamı 180°'den azdır. Eliptik geometri, 19. yüzyılda Alman matematikçi Bernhard Riemann tarafından geliştirildi; burada hiçbir paralel bulunamaz ve bir üçgenin iç açıların toplamı 180°'den fazladır. Riemann ayrıca üç tip geometriyi birleştiren ve büyük ölçüde genelleyen Riemann geometrisini geliştirdi ve eğri ile yüzey düşüncelerini genelleştiren bir manifold kavramını tanımladı.
19. yüzyıl, soyut cebirin başlangıcına dair büyük bir uğraşa tanık oldu. Almanya'daki Hermann Grassmann, vektör uzaylarının ilk versiyonunu verdi. İrlanda'daki William Rowan Hamilton değişmeli olmayan cebir geliştirdi. İngiliz matematikçi George Boole, kısa bir süre sonra Boole cebri olarak adlandırılan, rakamlarının sadece 0 ve 1 olduğu bir cebir geliştirdi. Boole cebri, matematiksel mantığın başlangıç noktasıdır ve elektrik mühendisliği ve bilgisayar bilimlerinde önemli uygulamaları vardır. Augustin-Louis Cauchy, Bernhard Riemann ve Karl Weierstrass, kalkülüsü daha titiz bir şekilde yeniden formüle etti.
Ayrıca ilk defa matematiğin sınırları araştırıldı. Norveçli Niels Henrik Abel ve bir Fransız olan Évariste Galois, dörtten büyük derecedeki polinom denklemlerini çözmek için genel bir cebirsel yöntem olmadığını kanıtladılar (Abel-Ruffini teoremi). Diğer 19. yüzyıl matematikçileri bunu, tek başına cetvel ve pergelle, verilen bir açıyı üçe bölmek, belirli bir küpün hacminin iki katı hacme sahip bir küp oluşturmak veya belirli bir alana sahip daireye eşit alana sahip bir kare oluşturmak için yeterli olmadığını kanıtlarken kullandılar. Antik Yunanlardan beri matematikçiler bu problemlerin hepsini boşuna çözmeye çalıştılar. Öte yandan, geometride üç boyutun sınırlaması, 19. yüzyılda parametre uzayı ve hiper karmaşık sayılar dikkate alınarak aşıldı.
Abel ve Galois'in çeşitli polinom denklemlerinin çözümlerine yönelik araştırmaları, grup teorisinin ve soyut cebirin ilişkili alanlarının daha fazla gelişmesi için zemin hazırladı. 20. yüzyılda fizikçiler ve diğer bilim adamları, grup teorisini simetriyi incelemenin ideal yolu olarak gördüler.
19. yüzyılın sonlarında, Georg Cantor sonsuzluk kavramının titiz bir şekilde ele alınmasını sağlayan ve neredeyse tüm matematiğin ortak dili haline gelen küme teorisinin ilk temellerini attı. Cantor'un küme teorisi ve matematiksel mantığın Peano, L.E.J. Brouwer, David Hilbert, Bertrand Russell ve A.N. Whitehead'in ellerinde yükselmesi, matematiğin temelleri üzerine uzun soluklu bir tartışma başlattı.
19. yüzyıl, bir dizi ulusal matematik toplumunun kurulmasına tanık oldu: 1865'te Londra Matematik Topluluğu, 1872'de Société Mathématique de France, 1884'te Circolo Matematico di Palermo, 1883'te Edinburgh Matematik Topluluğu ve 1888'de Amerikan Matematik Topluluğu kuruldu. İlk uluslararası, özel ilgi toplumu olan Kuaterniyon Derneği, bir vektör tartışması bağlamında 1899'da kuruldu.
1897'de Hensel p-sel sayıları tanıttı.[188]
20. yüzyıl
20. yüzyılda matematik büyük bir meslek haline geldi. Her yıl, matematikte binlerce yeni doktora ödülü verildi ve hem öğretimde hem de endüstride matematikle ilgili işler mevcuttu. Klein'in Matematiksel Bilimler Ansiklopedisinde matematiğin alanlarını ve uygulamalarını kataloglama çalışması yapılmıştır.
David Hilbert, 1900'de Uluslararası Matematikçiler Kongresi'nde yaptığı bir konuşmada matematikte çözülmemiş 23 problemin bir listesini çıkardı. Matematiğin birçok alanını kapsayan bu problemler, 20. yüzyıl matematiğinin çoğu için merkezi bir odak noktası oluşturdu. Bugün 10 tanesi çözüldü, 7 tanesi kısmen çözüldü ve 2 tanesi hala açıktır. Kalan 4 tanesi çözülmüş ya da çözülmemiş olarak ifade edilemeyecek kadar genel hatlarıyla formüle edilmiştir.

Önemli tarihsel varsayımlar nihayet kanıtlandı. 1976'da Wolfgang Haken ve Kenneth Appel, o zamanlar bir bilgisayarın bunu yapması tartışmalı olan dört renk teoremini ispatladılar. Andrew Wiles, başkalarının çalışmalarını temel alarak 1995 yılında Fermat'nın son teoremi kanıtladı. Paul Cohen ve Kurt Gödel, süreklilik hipotezinin küme teorisinin standart aksiyomlarından bağımsız olduğunu (ne kanıtlanabilir ne de çürütülebilir) kanıtladı. 1998'de Thomas Callister Hales, Kepler varsayımını kanıtladı.
Eşi görülmemiş büyüklük ve kapsamda matematiksel işbirlikleri gerçekleşti. Bir örnek olarak, 1955 ile 2004 yılları arasında ispatı yaklaşık 100 yazarın 500 küsur dergi makalesini gerektiren ve on binlerce sayfayı dolduran sonlu basit grupların sınıflandırılmasıdır ("muazzam teorem" olarak da adlandırılır). "Nicolas Bourbaki" takma adıyla yayın yapan Jean Dieudonné ve André Weil'in de aralarında bulunduğu bir grup Fransız matematikçi, bilinen tüm matematiği tutarlı ve titiz bir bütün olarak açıklamaya çalıştı. Elde edilen birkaç düzine cilt, matematik eğitimi üzerinde tartışmalı bir etkiye sahipti.[189]

Albert Einstein, genel görelilik teorisinde kullanmasıyla diferansiyel geometri hak ettiği yere geldi. Matematiksel mantık, topoloji ve John von Neumann'ın oyun teorisi gibi tamamen yeni matematik alanları, matematiksel yöntemlerle cevaplanabilecek soru türlerini değiştirdi. Her türlü yapı, aksiyomlar kullanılarak soyutlandı ve metrik uzaylar, topolojik uzaylar vb. gibi isimler verildi. Matematikçilerin yaptığı gibi, soyut bir yapı kavramının kendisi soyutlandı ve kategori teorisine yol açtı. Grothendieck ve Serre demet teorisini kullanarak cebirsel geometriyi yeniden biçimlendirdi. Poincaré'nin 1890'larda başlattığı dinamik sistemlerin nitel çalışmasında büyük ilerlemeler kaydedildi. Ölçü teorisi, 19. yüzyılın sonlarında ve 20. yüzyılın başlarında geliştirilmiştir. Ölçülerin uygulamaları arasında Lebesgue integrali, Kolmogorov'un olasılık teorisinin belitleştirilmesi ve ergodik teori bulunur. Düğüm teorisi büyük ölçüde genişledi. Kuantum mekaniği, fonksiyonel analizin geliştirilmesine yol açtı. Diğer yeni alanlar arasında Laurent Schwartz'ın dağılım teorisi, sabit nokta teorisi, tekillik teorisi, René Thom'un felaket teorisi, model teorisi ve Mandelbrot'un fraktalleri bulunmaktadır. Lie grupları ve Lie cebirleri ile Lie teorisi ana çalışma alanlarından biri haline geldi.
Abraham Robinson tarafından sunulan standart dışı analiz, gerçek sayılar alanını sonsuz küçük ve sonsuz büyüklükleri içeren Hiperreal sayılara doğru genişleterek, limit teorisi lehine itibarını yitirmiş olan kalkülüs için sonsuz küçük yaklaşımı rehabilite etti. Daha da büyük bir sayı sistemi olan gerçeküstü sayılar, kombinatoryal oyunlarla bağlantılı olarak John Horton Conway tarafından keşfedildi.
Bilgisayarların, önce mekanik analog makinelerde ve ardından dijital elektronik makinelerde geliştirilmesi ve sürekli iyileştirilmesi, endüstrinin seri üretimi, dağıtımı ve iletişimi kolaylaştırmak için gittikçe daha fazla miktarda veriyle uğraşmasına izin verdi ve bununla başa çıkmak için yeni matematik alanları geliştirildi: Alan Turing'in hesaplanabilirlik teorisi; karmaşıklık teorisi; Derrick Henry Lehmer'in sayı teorisini ve Lucas-Lehmer testini ilerletmek için ENIAC'ı kullanması; Rózsa Péter'in özyinelemeli fonksiyon teorisi; Claude Shannon'un bilgi teorisi; sinyal işleme; veri analizi; optimizasyon ve yöneylem araştırmasının diğer alanları. Önceki yüzyıllarda matematiksel odakların çoğu hesap ve sürekli fonksiyonlar üzerindeydi, ancak hesaplama ve iletişim ağlarının yükselişi, ayrık kavramların artan önemine ve graf teorisi dahil kombinatoriklerin genişlemesine yol açtı. Bilgisayarların hızı ve veri işleme yetenekleri, kalem ve kağıt hesaplamalarıyla uğraşmak için çok zaman alan matematik problemlerinin ele alınmasını da sağladı ve bu da sayısal analiz ve sembolik hesaplama gibi alanlara yol açtı. 20. yüzyılın en önemli yöntem ve algoritmalarından bazıları şunlardır: simpleks algoritma, hızlı Fourier dönüşümü, hata düzeltme kodları, kontrol teorisinden Kalman filtresi ve açık anahtar şifrelemesinin RSA algoritması.
Aynı zamanda matematiğin sınırlamaları hakkında derinlemesine kavrayışlar yapıldı. 1929 ve 1930'da, doğal sayılar artı toplama ve çarpma işlemlerinden biri hakkında formüle edilen tüm ifadelerin doğruluğunun veya yanlışlığının karar verilebilir olduğu, yani bir algoritma ile belirlenebileceği kanıtlandı. 1931'de Kurt Gödel, bunun doğal sayılar artı hem toplama hem de çarpma için geçerli olmadığını buldu; Peano aritmetiği olarak bilinen bu sistem aslında tamamlanamazdı. (Peano aritmetiği, asal sayı kavramı da dahil olmak üzere birçok sayı teorisi için yeterlidir.) Gödel'in iki eksiklik teoreminin bir sonucu, Peano aritmetiğini (tüm analiz ve geometri dahil) içeren herhangi bir matematiksel sistemde, hakikatin zorunlu olarak kanıtlanması aşmasıdır, yani sistem içinde kanıtlanamayan gerçek ifadeler vardır. Bu nedenle matematik matematiksel mantığa indirgenemez ve David Hilbert'in tüm matematiği eksiksiz ve tutarlı hale getirme hayalinin yeniden formüle edilmesi gerekir.
20. yüzyıl matematiğindeki en renkli şahsiyetlerden biri Srinivasa Aiyangar Ramanujan'dı (1887–1920), süper kompozit sayıların özellikleri, parçalanış fonksiyonu ve asimptotikleri ile sahte teta fonksiyonu dahil olmak üzere 3000'den fazla teoremi varsayan veya kanıtlayan Hint bir otodidakt (kendi kendini yetiştirmiş kimse)'dı. Ayrıca gama fonksiyonları, modüler formlar, ıraksak seriler, hipergeometrik seriler ve asal sayı teorisi alanlarında da büyük araştırmalar yaptı.

Paul Erdős, yüzlerce kişiyle birlikte çalışarak tarihteki diğer matematikçilerden daha fazla makale yayınladı. Matematikçilerin, matematikçileri bir Erdős sayısına götüren Kevin Bacon Oyununa eşdeğer bir oyunu vardır. Bu sayı, matematiksel makalelerin ortak yazarlığı ile ölçülen, bir kişi ile Paul Erdős arasındaki "işbirlikçi mesafeyi" açıklar.
.png.webp)
Emmy Noether birçokları tarafından matematik tarihindeki en önemli kadın olarak tanımlanmıştır.[190] Halkalar, alanlar ve cebir teorileri üzerinde çalıştı.
Çoğu çalışma alanında olduğu gibi, bilim çağındaki bilgi patlaması uzmanlaşmaya yol açtı: yüzyılın sonunda matematikte yüzlerce uzmanlık alanı vardı ve Matematik Konu Sınıflandırması düzinelerce sayfa uzunluğundaydı.[191] Giderek daha fazla matematik dergisi yayınlandı ve yüzyılın sonunda World Wide Web (İnternet)'in gelişimi çevrimiçi yayıncılığa yol açtı.
21. yüzyıl
2000 yılında Clay Matematik Enstitüsü yedi Milenyum Ödülü Problemini açıkladı ve 2003 yılında Poincaré varsayımı, (matematik kuruluşunu eleştirdiği için ödülü kabul etmeyi reddeden) Grigori Perelman tarafından çözüldü.
Çoğu matematiksel derginin artık çevrimiçi sürümlerinin yanı sıra basılı sürümleri de var ve yalnızca çevrimiçi olan birçok dergi yayınlanıyor. İlk olarak arXiv26 Ocak 2017 tarihinde Wayback Machine sitesinde arşivlendi. tarafından yaygınlaştırılan açık erişimli yayıncılığa doğru artan bir eğilim var.
Gelecek
Matematikte pek çok gözlemlenebilir eğilim vardır, bunlardan en önemlisi, konunun daha da büyümesi, bilgisayarların giderek daha önemli ve güçlü olması, matematiğin biyoenformatik uygulamalarının hızla artması, bilim ve endüstri tarafından üretilen verilerin hacmi (büyük veri), bunların bilgisayarlar tarafından işlenmesine/ele alınmasına olanak tanıdı ve kolaylaştırıldı, günümüzde bu durum patlayarak genişlemektedir.
Ayrıca bakınız
- Cebir Tarihi
- Kalkülüs tarihi
- Kombinatorik Tarihi
- Fonksiyon kavramının geçmişi
- Geometri tarihi
- Mantık tarihi
- Matematikçilerin Tarihi
- Matematiksel notasyonların tarihi
- Sayıların tarihi
- Sayı teorisinin tarihi
- İstatistiğin tarihi
- Trigonometri tarihi
- Sayıları yazmanın tarihi
- Matematik felsefesi
- Matematikteki önemli yayınların listesi
- Matematikçilerin listesi
- Matematik tarihi konularının listesi
- Matematik ödülleri listesi
- Matematiğin zaman çizelgesi
Notlar
- Boyer 1991, "Euclid of Alexandria" s. 119
- J. Friberg, "Methods and traditions of Babylonian mathematics. Plimpton 322, Pythagorean triples, and the Babylonian triangle parameter equations", Historia Mathematica, 8, 1981, ss. 277–318.
- Neugebauer, Otto (1969) [1957]. The Exact Sciences in Antiquity. Acta Historica Scientiarum Naturalium et Medicinalium. 2. 9. Dover Publications. ss. 1-191. ISBN 978-0-486-22332-2. PMID 14884919. 14 Ağustos 2020 tarihinde kaynağından arşivlendi. Erişim tarihi: 2 Eylül 2020. Chap. IV "Egyptian Mathematics and Astronomy", ss. 71–96.
- Heath (1931). "A Manual of Greek Mathematics". Nature. 128 (3235). s. 5. Bibcode:1931Natur.128..739T. doi:10.1038/128739a0.
- Sir Thomas L. Heath, A Manual of Greek Mathematics, Dover, 1963, s. 1: "Matematik söz konusu olduğunda, bilmek en önemli Yunan katkısıdır, çünkü matematiği ilk bilim yapan Yunanlardır."
- George Gheverghese Joseph, The Crest of the Peacock: Non-European Roots of Mathematics, Penguin Books, London, 1991, ss. 140–48
- Georges Ifrah, Universalgeschichte der Zahlen, Campus, Frankfurt/New York, 1986, ss. 428–37
- Robert Kaplan, "The Nothing That Is: A Natural History of Zero", Allen Lane/The Penguin Press, London, 1999
- "Her olası sayıyı, on sembolden (her sembolün bir basamak değerine ve mutlak bir değere sahip) kullanarak ifade etmenin ustaca yöntemi Hindistan'da ortaya çıktı. Fikir bugünlerde o kadar basit görünüyor ki anlamı ve derin önemi artık takdir edilmiyor. Basitliği, hesaplamayı kolaylaştırması ve aritmetiği en başta yararlı buluşlar arasına yerleştirmesinde yatmaktadır. Bu buluşun önemi, buluşun Antik Çağ'ın en büyük iki adamı Arşimet ve Apollonius'un ötesinde olduğu düşünüldüğünde daha kolay anlaşılır." – Pierre Simon Laplace http://www-history.mcs.st-and.ac.uk/HistTopics/Indian_numerals.html 17 Mayıs 2016 tarihinde Wayback Machine sitesinde arşivlendi.
- A.P. Juschkewitsch, "Geschichte der Mathematik im Mittelalter", Teubner, Leipzig, 1964
- "Arşivlenmiş kopya". 13 Ağustos 2020 tarihinde kaynağından arşivlendi. Erişim tarihi: 2 Eylül 2020.
- Boyer 1991, "Origins" s. 3
- Clark, J. (1975). Africa in Prehistory: Peripheral or Paramount? Man, 10(2), new series, ss.175-198. doi:10.2307/2800493
- "Arşivlenmiş kopya". 22 Eylül 2020 tarihinde kaynağından arşivlendi. Erişim tarihi: 2 Eylül 2020.
- Williams, Scott W. (2005). "The Oldest Mathematical Object is in Swaziland". Mathematicians of the African Diaspora. SUNY Buffalo mathematics department. 25 Mart 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 6 Mayıs 2006.
- Marshack, Alexander (1991): The Roots of Civilization, Colonial Hill, Mount Kisco, NY.
- Rudman, Peter Strom (2007). How Mathematics Happened: The First 50,000 Years. Prometheus Books. s. 64. ISBN 978-1-59102-477-4.
- Marshack, A. 1972. The Roots of Civilization: the Cognitive Beginning of Man’s First Art, Symbol and Notation. New York: McGraw-Hil
- Thom, Alexander, and Archie Thom, 1988, "The metrology and geometry of Megalithic Man", ss. 132–51 in C.L.N. Ruggles, ed., Records in Stone: Papers in memory of Alexander Thom. Cambridge University Press. 0-521-33381-4.
- Damerow, Peter (1996). "The Development of Arithmetical Thinking: On the Role of Calculating Aids in Ancient Egyptian & Babylonian Arithmetic". Abstraction & Representation: Essays on the Cultural Evolution of Thinking (Boston Studies in the Philosophy & History of Science). Springer. ISBN 0792338162. Erişim tarihi: 17 Ağustos 2019.
- Boyer 1991, "Mesopotamia" s. 24
- Boyer 1991, "Mesopotamia" s. 26
- Boyer 1991, "Mesopotamia" s. 25
- Boyer 1991, "Mesopotamia" s. 41
- Duncan J. Melville (2003). Third Millennium Chronology 7 Temmuz 2018 tarihinde Wayback Machine sitesinde arşivlendi., Third Millennium Mathematics. St. Lawrence University.
- Boyer 1991, "Mesopotamia" s. 27
- Aaboe, Asger (1998). Episodes from the Early History of Mathematics. New York: Random House. ss. 30-31.
- Boyer 1991, "Mesopotamia" s. 33
- Boyer 1991, "Mesopotamia" s. 39
- Boyer 1991, "Egypt" s. 11
- Egyptian Unit Fractions 6 Şubat 2010 tarihinde Wayback Machine sitesinde arşivlendi. at MathPages
- "Egyptian Unit Fractions". 1 Nisan 2016 tarihinde kaynağından arşivlendi. Erişim tarihi: 2 Eylül 2020.
- "Egyptian Papyri". www-history.mcs.st-andrews.ac.uk. 19 Şubat 2012 tarihinde kaynağından arşivlendi. Erişim tarihi: 2 Eylül 2020.
- "Egyptian Algebra – Mathematicians of the African Diaspora". www.math.buffalo.edu. 16 Nisan 2009 tarihinde kaynağından arşivlendi. Erişim tarihi: 2 Eylül 2020.
- Boyer 1991, "Egypt" s. 19
- "Egyptian Mathematical Papyri – Mathematicians of the African Diaspora". www.math.buffalo.edu. 7 Nisan 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 2 Eylül 2020.
- Howard Eves, An Introduction to the History of Mathematics, Saunders, 1990, 0-03-029558-0
- Boyer 1991, "The Age of Plato and Aristotle" s. 99
- Martin Bernal, "Animadversions on the Origins of Western Science", ss. 72–83 in Michael H. Shank, ed., The Scientific Enterprise in Antiquity and the Middle Ages, (Chicago: University of Chicago Press) 2000, s. 75.
- Boyer 1991, "Ionia and the Pythagoreans" s. 43
- Boyer 1991, "Ionia and the Pythagoreans" s. 49
- Eves, Howard, An Introduction to the History of Mathematics, Saunders, 1990, 0-03-029558-0.
- Kurt Von Fritz (1945). "The Discovery of Incommensurability by Hippasus of Metapontum". The Annals of Mathematics.
- James R. Choike (1980). "The Pentagram and the Discovery of an Irrational Number". The Two-Year College Mathematics Journal.
- Jane Qiu (7 Ocak 2014). "Ancient times table hidden in Chinese bamboo strips". Nature. doi:10.1038/nature.2014.14482. 13 Eylül 2019 tarihinde kaynağından arşivlendi. Erişim tarihi: 15 Eylül 2014.
- David E. Smith (1958), History of Mathematics, Volume I: General Survey of the History of Elementary Mathematics, New York: Dover Publications (a reprint of the 1951 publication), 0-486-20429-4, ss. 58, 129.
- David E. Smith (1958), History of Mathematics, Volume I: General Survey of the History of Elementary Mathematics, New York: Dover Publications (a reprint of the 1951 publication), 0-486-20429-4, s. 129.
- Boyer 1991, "The Age of Plato and Aristotle" s. 86
- Boyer 1991, "The Age of Plato and Aristotle" s. 88
- Calian, George F. (2014). "One, Two, Three… A Discussion on the Generation of Numbers" (PDF). New Europe College. 15 Ekim 2015 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 2 Eylül 2020.
- Boyer 1991, "The Age of Plato and Aristotle" s. 87
- Boyer 1991, "The Age of Plato and Aristotle" s. 92
- Boyer 1991, "The Age of Plato and Aristotle" s. 93
- Boyer 1991, "The Age of Plato and Aristotle" s. 91
- Boyer 1991, "The Age of Plato and Aristotle" s. 98
- Bill Casselman. "One of the Oldest Extant Diagrams from Euclid". University of British Columbia. 4 Haziran 2012 tarihinde kaynağından arşivlendi. Erişim tarihi: 26 Eylül 2008.
- Boyer 1991, "Euclid of Alexandria" s. 100
- Boyer 1991, "Euclid of Alexandria" s. 104
- Howard Eves, An Introduction to the History of Mathematics, Saunders, 1990, 0-03-029558-0 s. 141: "No work, except The Bible, has been more widely used...."
- Boyer 1991, "Euclid of Alexandria" s. 102
- Boyer 1991, "Archimedes of Syracuse" s. 120
- Boyer 1991, "Archimedes of Syracuse" s. 130
- Boyer 1991, "Archimedes of Syracuse" s. 126
- Boyer 1991, "Archimedes of Syracuse" s. 125
- Boyer 1991, "Archimedes of Syracuse" s. 121
- Boyer 1991, "Archimedes of Syracuse" s. 137
- Boyer 1991, "Apollonius of Perga" s. 145
- Boyer 1991, "Apollonius of Perga" s. 146
- Boyer 1991, "Apollonius of Perga" s. 152
- Boyer 1991, "Apollonius of Perga" s. 156
- Boyer 1991, "Greek Trigonometry and Mensuration" s. 161
- Boyer 1991, "Greek Trigonometry and Mensuration" s. 175
- Boyer 1991, "Greek Trigonometry and Mensuration" s. 162
- S.C. Roy. Complex numbers: lattice simulation and zeta function applications, s. 1 21 Ağustos 2018 tarihinde Wayback Machine sitesinde arşivlendi.. Harwood Publishing, 2007, 131 sayfa. 1-904275-25-7
- Boyer 1991, "Greek Trigonometry and Mensuration" s. 163
- Boyer 1991, "Greek Trigonometry and Mensuration" s. 164
- Boyer 1991, "Greek Trigonometry and Mensuration" s. 168
- Boyer 1991, "Revival and Decline of Greek Mathematics" s. 178
- Boyer 1991, "Revival and Decline of Greek Mathematics" s. 180
- Boyer 1991, "Revival and Decline of Greek Mathematics" s. 181
- Boyer 1991, "Revival and Decline of Greek Mathematics" s. 183
- Boyer 1991, "Revival and Decline of Greek Mathematics" ss. 183–90
- Elbert Hubbard, (1894), Little Journeys To The Homes Of Great Teachers, s.176, http://www.gutenberg.org/ebooks/18936 6 Mayıs 2019 tarihinde Wayback Machine sitesinde arşivlendi.
- Bernardi, G. (2016). Hypatia of Alexandria (355 or 370 ca. to 415). In The Unforgotten Sisters (ss. 27-36). Springer, Cham.
- "Internet History Sourcebooks Project". sourcebooks.fordham.edu. 12 Kasım 2016 tarihinde kaynağından arşivlendi. Erişim tarihi: 2 Eylül 2020.
- Boyer 1991, "Revival and Decline of Greek Mathematics" ss. 190–94
- Boyer 1991, "Revival and Decline of Greek Mathematics" s. 193
- Boyer 1991, "Revival and Decline of Greek Mathematics" s. 194
- Goodman 2016, s. 119
- Cuomo 2001, ss. 194, 204–06
- Cuomo 2001, ss. 192–95
- Goodman 2016, ss. 120–21
- Cuomo 2001, s. 196
- Cuomo 2001, ss. 207–08
- Goodman 2016, ss. 119–20
- Tang 2005, ss. 14–15, 45
- Joyce 1979, s. 256
- Gullberg 1997, s. 17
- Gullberg 1997, ss. 17–18
- Gullberg 1997, s. 18
- Gullberg 1997, ss. 18–19
- Needham & Wang 2000, ss. 281–85
- Needham & Wang 2000, s. 285
- Sleeswyk 1981, ss. 188–200
- Boyer 1991, "China and India" s. 201
- Boyer 1991, "China and India" s. 196
- Katz 2007, ss. 194–99
- Boyer 1991, "China and India" s. 198
- Needham & Wang 1995, ss. 91–92
- Needham & Wang 1995, s. 94
- Needham & Wang 1995, s. 22
- Straffin 1998, s. 164
- Needham & Wang 1995, ss. 99–100
- Berggren, Borwein & Borwein 2004, s. 27
- Crespigny 2007, s. 1050
- Boyer 1991, "China and India" s. 202
- Needham & Wang 1995, ss. 100–01
- Berggren, Borwein & Borwein 2004, ss. 20, 24–26
- Zill, Dennis G.; Wright, Scott; Wright, Warren S. (2009). Calculus: Early Transcendentals. 3. Jones & Bartlett Learning. s. xxvii. ISBN 978-0-7637-5995-7. 21 Nisan 2019 tarihinde kaynağından arşivlendi. Erişim tarihi: 2 Eylül 2020. Extract of s. 27 21 Nisan 2019 tarihinde Wayback Machine sitesinde arşivlendi.
- O'Connor, John J.; Robertson, Edmund F., "Li Zhi", MacTutor History of Mathematics archive, University of St Andrews.
- Boyer 1991, "China and India" s. 205
- Volkov 2009, ss. 153–56
- Volkov 2009, ss. 154–55
- Volkov 2009, ss. 156–57
- Volkov 2009, s. 155
- Development Of Modern Numerals And Numeral Systems: The Hindu-Arabic system 29 Aralık 2017 tarihinde Wayback Machine sitesinde arşivlendi., Encyclopaedia Britannica, Quote: "1, 4 ve 6 Ashoka yazıtlarında bulunur (M.Ö. 3. yüzyıl); 2, 4, 6, 7 ve 9, yaklaşık bir yüzyıl sonra Nana Ghat yazıtlarında görülür; ve MS 1. veya 2. yüzyıl Nasik mağaralarındaki 2, 3, 4, 5, 6, 7 ve 9 -hepsi bugününkilere önemli ölçüde benzeyen biçimlerde, 2 ve 3, eski = ve ≡'den iyi tanınan el yazısı türevleridir."
- Boyer 1991, "China and India" s. 206
- Boyer 1991, "China and India" s. 207
- Puttaswamy, T.K. (2000). "The Accomplishments of Ancient Indian Mathematicians". Selin, Helaine; D'Ambrosio, Ubiratan (Edl.). Mathematics Across Cultures: The History of Non-western Mathematics. Springer. ss. 411-12. ISBN 978-1-4020-0260-1.
- Kulkarni, R.P. (1978). "The Value of π known to Śulbasūtras" (PDF). Indian Journal of History of Science. 13 (1). ss. 32-41. 6 Şubat 2012 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 2 Eylül 2020.
- Connor, J.J.; Robertson, E.F. "The Indian Sulbasutras". Univ. of St. Andrew, Scotland. 23 Ocak 2001 tarihinde kaynağından arşivlendi. Erişim tarihi: 2 Eylül 2020.
- Bronkhorst, Johannes (2001). "Panini and Euclid: Reflections on Indian Geometry". Journal of Indian Philosophy. 29 (1–2). ss. 43-80. doi:10.1023/A:1017506118885.
- Kadvany, John (8 Şubat 2008). "Positional Value and Linguistic Recursion". Journal of Indian Philosophy (İngilizce). 35 (5–6). ss. 487-520. CiteSeerX 10.1.1.565.2083 $2. doi:10.1007/s10781-007-9025-5. ISSN 0022-1791.
- Sanchez, Julio; Canton, Maria P. (2007). Microcontroller programming : the microchip PIC. Boca Raton, Florida: CRC Press. s. 37. ISBN 978-0-8493-7189-9.
- W.S. Anglin and J. Lambek, The Heritage of Thales, Springer, 1995, 0-387-94544-X
- Hall, Rachel W. (2008). "Math for poets and drummers" (PDF). Math Horizons. 15 (3). ss. 10-11. doi:10.1080/10724117.2008.11974752. 9 Ağustos 2017 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 2 Eylül 2020.
- Boyer 1991, "China and India" s. 208
- Boyer 1991, "China and India" s. 209
- Boyer 1991, "China and India" s. 210
- Boyer 1991, "China and India" s. 211
- Boyer (1991). "The Arabic Hegemony". History of Mathematics. s. 226.
766'da Araplar tarafından Sindhind olarak bilinen astronomik-matematiksel bir çalışmanın Hindistan'dan Bağdat'a getirildiğini öğreniyoruz. Genelde bunun Brahmasphuta Siddhanta olduğu düşünülse de Surya Siddhanata da olabilir. Birkaç yıl sonra, belki yaklaşık 775'de, Siddhanata Arapçaya çevrildi ve kısa süre sonra (y. 780'de) Batlamyus'un astrolojik Tetrabiblos adlı eseri Yunanca'dan Arapça'ya çevrildi.
- Edwards, A.W.F. (2013) The Arithmetical Triangle. In: Wilson, R. and Watkins, J.J., Eds., Combinatorics: Ancient and Modern, Oxford University Press, Oxford, ss. 166-180. http://dx.doi.org/10.1093/acprof:oso/9780199656592.003.0008
- Plofker 2009 182–207
- Plofker 2009 ss. 197–98; George Gheverghese Joseph, The Crest of the Peacock: Non-European Roots of Mathematics, Penguin Books, London, 1991 ss. 298–300; Takao Hayashi, Indian Mathematics, ss. 118–30 in Companion History of the History and Philosophy of the Mathematical Sciences, ed. I. Grattan.Guinness, Johns Hopkins University Press, Baltimore and London, 1994, s. 126
- Plofker 2009 ss. 217–53
- C. K. Raju (2001). "Computers, mathematics education, and the alternative epistemology of the calculus in the Yuktibhāṣā" (PDF). Philosophy East & West. 51 (3). ss. 325-362. doi:10.1353/pew.2001.0045. 4 Kasım 2019 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 11 Şubat 2020.
- P.P. Divakaran, The first textbook of calculus: Yukti-bhāṣā, Journal of Indian Philosophy 35, 2007, ss. 417–33.
- C. K. Raju (2007). Cultural foundations of mathematics: the nature of mathematical proof and the transmission of the calculus from india to europe in the 16th c. CE. Delhi: Pearson Longman.
- D F Almeida, J K John and A Zadorozhnyy (2001). "Keralese mathematics: its possible transmission to Europe and the consequential educational implications". Journal of Natural Geometry. 20 (1). ss. 77-104.
- Pingree, David (Aralık 1992). "Hellenophilia versus the History of Science". Isis. 83 (4). ss. 554-563. Bibcode:1992Isis...83..554P. doi:10.1086/356288. JSTOR 234257.
Size verebileceğim bir örnek, Hint Mādhava'nın geometrik ve cebirsel argümanlar kullanarak trigonometrik fonksiyonların sonsuz güç serilerinin yaklaşık MS 1400'de gösterimi ile ilgilidir. Bu, 1830'larda Charles Whish tarafından İngilizce olarak ilk kez tanımlandığında, Hintlerin hesabı keşfi olarak müjdelendi. Bu iddia ve Mādhava'nın başarıları, Batılı tarihçiler tarafından, muhtemelen ilk başta bir Hintin hesabı keşfettiğini kabul edemedikleri için, ancak daha sonra kimse Whish'in yayınlanan makalesinin yer aldığı Kraliyet Asya Toplumu İşlemlerini okumadığı için göz ardı edildi. Konu 1950'lerde yeniden su yüzüne çıktı ve şimdi Sanskritçe metinleri düzgün bir şekilde düzenledik ve Mādhava'nın diziyi hesaplama olmadan türetmesinin akıllıca yolunu anlıyoruz; ancak birçok tarihçi, problemi ve çözümünü kalkülüs dışında herhangi bir terimle kavramayı hala imkansız buluyor ve Mādhava'nın bulduğu şeyin analiz olduğunu ilan ediyor. Bu durumda, Mādhava'nın matematiğinin zarafeti ve parlaklığı, alternatif ve güçlü bir çözüm keşfettiği bir problemin mevcut matematiksel çözümünün altına gömüldükçe çarpıtılmaktadır.
- Bressoud, David (2002). "Was Calculus Invented in India?". College Mathematics Journal. 33 (1). ss. 2-13. doi:10.2307/1558972. JSTOR 1558972.
- Plofker, Kim (Kasım 2001). "The 'Error' in the Indian "Taylor Series Approximation" to the Sine". Historia Mathematica. 28 (4). s. 293. doi:10.1006/hmat.2001.2331.
Hint matematiği tartışmalarında "türev kavramı [Hindistan'da] Manjula zamanında (... 10. yüzyılda) anlaşıldı" [Joseph 1991, 300] gibi iddialara rastlamak alışılmadık bir durum değildir. "Madhava'nın matematiksel analizin kurucusu olduğunu düşünebiliriz" (Joseph 1991, 293) veya Bhaskara II'nin "diferansiyel analiz ilkesinin keşfinde Newton ve Leibniz'in öncüsü" olduğu iddia edilebilir (Bag 1979 , 294) .... Özellikle erken Avrupa hesabı ile Keralese'nin güç serileri üzerine çalışması arasındaki benzer noktalar, 15. yüzyılda veya sonrasında Malabar kıyılarından Latin bilim adamlarına matematiksel fikirlerin olası aktarımına dair önerilere bile ilham vermiştir. Dünya (örneğin, (Bag 1979, 285)) .... Bununla birlikte, Sanskritçe (veya Malayalam) ve Latin matematiğinin benzerliğine yapılan bu tür bir vurgunun, orjinini görme ve kavrama yeteneğimizi tamamen azaltma riski taşıdığı akılda tutulmalıdır. Hint'in 'diferansiyel hesap ilkesinin keşfinden' bahsetmek, Sinüs'teki değişiklikleri kosinüs aracılığıyla ifade etmek için Hint tekniklerinin ya da tam tersi, gördüğümüz örneklerde olduğu gibi, belirli trigonometrik bağlam içinde kaldığı gerçeğini biraz gizler. Diferansiyel 'ilke', keyfi fonksiyonlara genelleştirilmemiştir - aslında, keyfi bir fonksiyonun açık kavramı, türevinden veya türevi almak için bir algoritmadan bahsetmemek, burada alakasızdır.
- Katz, Victor J. (Haziran 1995). "Ideas of Calculus in Islam and India" (PDF). Mathematics Magazine. 68 (3). ss. 163-74. doi:10.2307/2691411. JSTOR 2691411. 4 Mart 2016 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 2 Eylül 2020.
- Boyer 1991, "The Arabic Hegemony" s. 230 "Yukarıda verilen altı denklem durumu, pozitif köke sahip doğrusal ve ikinci dereceden denklemlerin tüm olasılıklarını tüketir. El-Harezmi'nin açıklaması o kadar sistematik ve kapsamlıydı ki okuyucuları çözümlere hakim olma konusunda çok az zorluk çekmiş olmalıdır."
- Gandz and Saloman (1936), The sources of Khwarizmi's algebra, Osiris i, ss. 263–77: "Bir anlamda Harizmi, Diophantus'tan daha çok "cebirin babası" olarak anılmaya hak kazanmıştır çünkü Harizmi, cebiri temel bir biçimde ve kendi iyiliği için öğreten ilk kişidir, Diophantus öncelikle sayılar teorisiyle ilgilenir."
- Boyer 1991, "The Arabic Hegemony" s. 229 "El-Cebr ve mukabele terimlerinin ne anlama geldiği kesin değildir, ancak olağan yorum yukarıdaki çeviride ima edilene benzerdir. El-Cebr kelimesi muhtemelen "restorasyon" veya "tamamlama" gibi bir anlama geliyordu ve çıkarılan terimlerin denklemin diğer tarafına aktarılmasına atıfta bulunuyor gibi görünüyor; "mukabele" kelimesinin "indirgeme" veya "dengeleme" anlamına geldiği söylenir - yani denklemin zıt taraflarındaki benzer terimlerin iptali."
- Rashed, R.; Armstrong, Angela (1994). The Development of Arabic Mathematics. Springer. ss. 11-12. ISBN 978-0-7923-2565-9. OCLC 29181926.
- Sesiano, Jacques (1997). "Abū Kāmil". Encyclopaedia of the history of science, technology, and medicine in non-western cultures. Springer. ss. 4-5.
- Roshdi Rashed, Histoire des sciences arabe, cilt 2, 1997, ss.102-105
- Katz 1998, ss. 255–59
- F. Woepcke (1853). Extrait du Fakhri, traité d'Algèbre par Abou Bekr Mohammed Ben Alhacan Alkarkhi. Paris.
- Katz, Victor J. (1995). "Ideas of Calculus in Islam and India". Mathematics Magazine. 68 (3). ss. 163-74. doi:10.2307/2691411. JSTOR 2691411.
- Alam, S (2015). "Mathematics for All and Forever" (PDF). Indian Institute of Social Reform & Research International Journal of Research. 21 Nisan 2018 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 2 Eylül 2020.
- O'Connor, John J.; Robertson, Edmund F., "Abu'l Hasan ibn Ali al Qalasadi", MacTutor History of Mathematics archive, University of St Andrews.
- Goodman 2016, s. 121
- Wisdom, 11:21
- Caldwell, John (1981) "The De Institutione Arithmetica and the De Institutione Musica", ss. 135–54 in Margaret Gibson, ed., Boethius: His Life, Thought, and Influence, (Oxford: Basil Blackwell).
- Folkerts, Menso, "Boethius" Geometrie II, (Wiesbaden: Franz Steiner Verlag, 1970).
- Marie-Thérèse d'Alverny, "Translations and Translators", ss. 421–62 in Robert L. Benson and Giles Constable, Renaissance and Renewal in the Twelfth Century, (Cambridge: Harvard University Press, 1982).
- Guy Beaujouan, "The Transformation of the Quadrivium", ss. 463–87 in Robert L. Benson and Giles Constable, Renaissance and Renewal in the Twelfth Century, (Cambridge: Harvard University Press, 1982).
- Grant, Edward and John E. Murdoch (1987), eds., Mathematics and Its Applications to Science and Natural Philosophy in the Middle Ages, (Cambridge: Cambridge University Press) 0-521-32260-X.
- Clagett, Marshall (1961) The Science of Mechanics in the Middle Ages, (Madison: University of Wisconsin Press), ss. 421–40.
- Murdoch, John E. (1969) "Mathesis in Philosophiam Scholasticam Introducta: The Rise and Development of the Application of Mathematics in Fourteenth Century Philosophy and Theology", in Arts libéraux et philosophie au Moyen Âge (Montréal: Institut d'Études Médiévales), at ss. 224–27.
- Pickover, Clifford A. (2009), The Math Book: From Pythagoras to the 57th Dimension, 250 Milestones in the History of Mathematics, Sterling Publishing Company, Inc., s. 104, ISBN 978-1-4027-5796-9, 2 Ağustos 2019 tarihinde kaynağından arşivlendi, erişim tarihi: 2 Eylül 2020,
Nicole Oresme ... harmonik serinin ıraksamasını kanıtlayan ilk kişiydi (y. 1350). Sonuçları birkaç yüzyıl boyunca kayboldu ve sonuçlar, 1647'de İtalyan matematikçi Pietro Mengoli ve 1687'de İsviçreli matematikçi Johann Bernoulli tarafından tekrar kanıtlandı.
- Clagett, Marshall (1961) The Science of Mechanics in the Middle Ages, (Madison: University of Wisconsin Press), ss. 210, 214–15, 236.
- Clagett, Marshall (1961) The Science of Mechanics in the Middle Ages, (Madison: University of Wisconsin Press), s. 284.
- Clagett, Marshall (1961) The Science of Mechanics in the Middle Ages, (Madison: University of Wisconsin Press), ss. 332–45, 382–91.
- Nicole Oresme, "Questions on the Geometry of Euclid" Q. 14, ss. 560–65, in Marshall Clagett, ed., Nicole Oresme and the Medieval Geometry of Qualities and Motions, (Madison: University of Wisconsin Press, 1968).
- Heeffer, Albrecht: On the curious historical coincidence of algebra and double-entry bookkeeping, Foundations of the Formal Sciences, Ghent University, November 2009, s. 7 20 Ağustos 2011 tarihinde Wayback Machine sitesinde arşivlendi.
- della Francesca, Piero. De Prospectiva Pingendi, ed. G. Nicco Fasola, 2 vols., Florence (1942).
- della Francesca, Piero. Trattato d'Abaco, ed. G. Arrighi, Pisa (1970).
- della Francesca, Piero. L'opera "De corporibus regularibus" di Pietro Franceschi detto della Francesca usurpata da Fra Luca Pacioli, ed. G. Mancini, Rome, (1916).
- Alan Sangster, Greg Stoner & Patricia McCarthy: "The market for Luca Pacioli’s Summa Arithmetica" 26 Ocak 2018 tarihinde Wayback Machine sitesinde arşivlendi. (Accounting, Business & Financial History Conference, Cardiff, September 2007) ss. 1–2
- Grattan-Guinness, Ivor (1997). The Rainbow of Mathematics: A History of the Mathematical Sciences. W.W. Norton. ISBN 978-0-393-32030-5.
- Kline, Morris (1953). Mathematics in Western Culture. Great Britain: Pelican. ss. 150-51.
- Struik, Dirk (1987). A Concise History of Mathematics. 3. Courier Dover Publications. ss. 89. ISBN 978-0-486-60255-4.
- Eves, Howard, An Introduction to the History of Mathematics, Saunders, 1990, 0-03-029558-0, s. 379, "... kalkülüs kavramları ... o kadar kapsamlı ve modern dünya üzerinde öylesine bir etki yarattı ki, bugün onlar hakkında biraz bilgi sahibi olmadan bir insanın iyi eğitimli olduğunu pek iddia edemeyeceğini söylemek belki de doğrudur."
- K. İlhan İkeda, Serdar Nair & Ergin Süer (21-25 Ağustos 2017). "p-SEL SAYILAR" (PDF). Eskişehir: Çakılarası Matematik Köyü.
- Maurice Mashaal, 2006. Bourbaki: A Secret Society of Mathematicians. American Mathematical Society. 0-8218-3967-5.
- Alexandrov, Pavel S. (1981), "In Memory of Emmy Noether", Brewer, James W; Smith, Martha K (Edl.), Emmy Noether: A Tribute to Her Life and Work, New York: Marcel Dekker, ss. 99-111, ISBN 978-0-8247-1550-2.
- "Mathematics Subject Classification 2000" (PDF). 18 Ekim 2011 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 2 Eylül 2020.
Dipnotlar
- π'nin yaklaşık değerleri, (3,0044...), (3,125), (3,11418685...), (3,202216...), ve (3,1389)'dir.
Kaynakça
- Berggren, Lennart; Borwein, Jonathan M.; Borwein, Peter B. (2004), Pi: A Source Book, New York: Springer, ISBN 978-0-387-20571-7
- Boyer, C.B. (1991) [1989], A History of Mathematics (2. bas.), New York: Wiley, ISBN 978-0-471-54397-8
- Cuomo, Serafina (2001), Ancient Mathematics, Londra: Routledge, ISBN 978-0-415-16495-5
- Eves, Howard (1990), An Introduction to the History of Mathematics, Saunders, ISBN 0-03-029558-0
- Goodman, Michael, K.J. (2016), An introduction of the Early Development of Mathematics, Hoboken: Wiley, ISBN 978-1-119-10497-1
- Gullberg, Jan (1997), Mathematics: From the Birth of Numbers, New York: W.W. Norton and Company, ISBN 978-0-393-04002-9
- Joyce, Hetty (July 1979), "Form, Function and Technique in the Pavements of Delos and Pompeii", American Journal of Archaeology, 83 (3), ss. 253-63, doi:10.2307/505056, JSTOR 505056.
- Katz, Victor J. (1998), A History of Mathematics: An Introduction (2. bas.), Addison-Wesley, ISBN 978-0-321-01618-8
- Katz, Victor J. (2007), The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook, Princeton, NJ: Princeton University Press, ISBN 978-0-691-11485-9
- Needham, Joseph; Wang, Ling (1995) [1959], Science and Civilization in China: Mathematics and the Sciences of the Heavens and the Earth, 3, Cambridge: Cambridge University Press, ISBN 978-0-521-05801-8
- Needham, Joseph; Wang, Ling (2000) [1965], Science and Civilization in China: Physics and Physical Technology: Mechanical Engineering, 4 (reprint bas.), Cambridge: Cambridge University Press, ISBN 978-0-521-05803-2
- Sleeswyk, Andre (October 1981), "Vitruvius' odometer", Scientific American, 252 (4), ss. 188-200, Bibcode:1981SciAm.245d.188S, doi:10.1038/scientificamerican1081-188.
- Straffin, Philip D. (1998), "Liu Hui and the First Golden Age of Chinese Mathematics", Mathematics Magazine, 71 (3), ss. 163-81, doi:10.1080/0025570X.1998.11996627
- Tang, Birgit (2005), Delos, Carthage, Ampurias: the Housing of Three Mediterranean Trading Centres, Rome: L'Erma di Bretschneider (Accademia di Danimarca), ISBN 978-88-8265-305-7.
- Volkov, Alexei (2009), "Mathematics and Mathematics Education in Traditional Vietnam", Robson, Eleanor; Stedall, Jacqueline (Edl.), The Oxford Handbook of the History of Mathematics, Oxford: Oxford University Press, ss. 153-76, ISBN 978-0-19-921312-2
- Matematiğin Zaman Çizelgesi13 Ağustos 2020 tarihinde Wayback Machine sitesinde arşivlendi.
İlave okumalar
Genel
- Aaboe, Asger (1964). Episodes from the Early History of Mathematics. New York: Random House.
- Bell, E.T. (1937). Men of Mathematics. Simon and Schuster.
- Burton, David M. The History of Mathematics: An Introduction. McGraw Hill: 1997.
- Grattan-Guinness, Ivor (2003). Companion Encyclopedia of the History and Philosophy of the Mathematical Sciences. The Johns Hopkins University Press. ISBN 978-0-8018-7397-3.
- Kline, Morris. Mathematical Thought from Ancient to Modern Times.
- Struik, D.J. (1987). A Concise History of Mathematics, fourth revised edition. Dover Publications, New York.
Belirli bir döneme ait kitaplar
- Gillings, Richard J. (1972). Mathematics in the Time of the Pharaohs. Cambridge, MA: MIT Press.
- Heath, Sir Thomas (1981). A History of Greek Mathematics. Dover. ISBN 978-0-486-24073-2.
- van der Waerden, B.L., Geometry and Algebra in Ancient Civilizations, Springer, 1983, 0-387-12159-5.
Belirli bir konudaki kitaplar
- Hoffman, Paul (1998). The Man Who Loved Only Numbers: The Story of Paul Erdős and the Search for Mathematical Truth. Hyperion. ISBN 0-7868-6362-5.
- Menninger, Karl W. (1969). Number Words and Number Symbols: A Cultural History of Numbers. MIT Press. ISBN 978-0-262-13040-0.
- Stigler, Stephen M. (1990). The History of Statistics: The Measurement of Uncertainty before 1900. Belknap Press. ISBN 978-0-674-40341-3.
Dış bağlantılar
| Vikisöz'de Matematik tarihi ile ilgili sözleri bulabilirsiniz. |
Belgeseller
- BBC (2008). The Story of Maths.
- "Renaissance Mathematics". 10 Ağustos 2020 tarihinde kaynağından arşivlendi.
Robert Kaplan, Jim Bennett & Jackie Stedall ile BBC Radio 4 tartışma programı; (In Our Time, Jun 2, 2005) - "Matematiğin Aydınlık Dünyası". Erişim tarihi: 6 Şubat 2021.
Eğitim materyalleri
- John J. O'Connor & Edmund F. Robertson. "MacTutor History of Mathematics archive". Scotland: University of St Andrews. 16 Eylül 2013 tarihinde kaynağından arşivlendi.
(Pek çok tarihsel ve çağdaş matematikçi hakkında ayrıntılı biyografilerin yanı sıra matematik tarihindeki önemli eğriler ve çeşitli konular hakkında bilgiler içeren ödüllü bir web sitesi.)
- David E. Joyce. "History of Mathematics Home Page". Clark University. 25 Nisan 2007 tarihinde kaynağından arşivlendi.
(Kapsamlı bir bibliyografya ile matematik tarihindeki çeşitli konularda makaleler.)
- David R. Wilkins. "The History of Mathematics". Trinity College, Dublin. 28 Nisan 2007 tarihinde kaynağından arşivlendi.
(17. ve 19. yüzyıllar arasında matematik üzerine materyal koleksiyonları.)
- Jeff Miller. "Earliest Known Uses of Some of the Words of Mathematics". 4 Mart 2009 tarihinde kaynağından arşivlendi.
(Matematikte kullanılan terimlerin bilinen en eski kullanımları hakkında bilgi içerir.)
- Jeff Miller. "Earliest Uses of Various Mathematical Symbols". 20 Şubat 2016 tarihinde kaynağından arşivlendi.
(Matematiksel gösterimlerin tarihi hakkında bilgi içerir.)
- John Aldrich. "Mathematical Words: Origins and Sources". University of Southampton. 1 Ağustos 2009 tarihinde kaynağından arşivlendi.
(Modern matematiksel kelime deposunun kökenlerini tartışır.)
- Larry Riddle. "Biographies of Women Mathematicians". Agnes Scott College. 23 Şubat 2011 tarihinde kaynağından arşivlendi.
- Scott W. Williams. "Mathematicians of the African Diaspora". University at Buffalo. 28 Ekim 2005 tarihinde kaynağından arşivlendi.
- V. Frederick Rickey & Victor J. Katz (2009). "Notes for MAA minicourse: teaching a course in the history of mathematics" (PDF). 1 Aralık 2018 tarihinde kaynağından (PDF) arşivlendi.
Bibliyografyalar
- Steven W. Rockey. "A Bibliography of Collected Works and Correspondence of Mathematicians". Cornell University Library. 25 Nisan 2017 tarihinde kaynağından arşivlendi.
Organizasyonlar
- "International Commission for the History of Mathematics". 7 Ocak 2011 tarihinde kaynağından arşivlendi.
Dergiler
- "Historia Mathematica". 10 Ağustos 2020 tarihinde kaynağından arşivlendi.
- "Convergence". Math History Magazine. Mathematical Association of America. 8 Eylül 2020 tarihinde kaynağından arşivlendi.
- "History of Mathematics". Math Archives. Knoxville: University of Tennessee. 4 Ekim 2006 tarihinde kaynağından arşivlendi.
- "History/Biography". The Math Forum. Drexel University. 7 Mayıs 2007 tarihinde kaynağından arşivlendi.
- "History of Mathematics". Courtright Memorial Library. 16 Temmuz 2002 tarihinde kaynağından arşivlendi.
- David Calvis. "History of Mathematics Web Sites". Baldwin-Wallace College. 25 Mayıs 2009 tarihinde kaynağından arşivlendi.
- Curlie'de History of mathematics (DMOZ tabanlı)
- "Historia de las Matemáticas". Universidad de La La guna. 19 Şubat 2003 tarihinde kaynağından arşivlendi.
- "História da Matemática". Universidade de Coimbra. 15 Temmuz 2009 tarihinde kaynağından arşivlendi.
- "Using History in Math Class". 7 Temmuz 2011 tarihinde kaynağından arşivlendi.
- Bruno Kevius. "Mathematical Resources: History of Mathematics". 11 Temmuz 2020 tarihinde kaynağından arşivlendi.
- Roberta Tucci. "History of Mathematics". 15 Haziran 2008 tarihinde kaynağından arşivlendi.
- "Matematik Dünyası". 8 Ağustos 2020 tarihinde kaynağından arşivlendi.





_-_Putto_with_a_Personification_of_Mathematics_-_960269_-_National_Trust.jpg.webp)
