Gnomon teoremi
Gnomon teoremi, bir gnomon'da meydana gelen belirli paralelkenarların eşit büyüklükte alanlara sahip olduğunu belirtir. Gnomon (Grekçe: γνώμων), geometride benzer bir paralelkenarı daha büyük bir paralelkenarın bir köşesinden çıkararak oluşturulan bir düzlem şeklidir; veya daha genel olarak, belirli bir şekle eklendiğinde, aynı şekle sahip daha büyük bir şekil oluşturan bir şekildir.[1]

Gnomon Teoremi: yeşil alan = kırmızı alan,
Teorem
köşegeni üzerinde noktası olan bir paralelkenarında kenarına paralel olan ve noktasından geçen doğru, kenarını noktasında ve kenarını da noktasında keser. Benzer şekilde kenarına paralel ve noktasından geçen doğru, kenarını noktasında ve kenarını da noktasında keser. Gnomon teoremi, ve paralelkenarlarının eşit alanlara sahip olduğunu belirtir.[2][3]
Gnomon, üst üste gelen iki paralelkenar olan ve 'den oluşan L biçimindeki şeklin adıdır. Eşit alana sahip ve paralelkenarları, ve köşegenlerindeki paralelkenarların tamamlayıcısı olarak adlandırılır.[4]
İspat
Teoremin kanıtı, ana paralelkenarın alanları ve köşegeninin etrafındaki iki iç paralelkenarın alanları göz önüne alındığında basittir:
- ilk olarak, ana paralelkenar ile iki iç paralelkenar arasındaki fark, iki tamamlayıcının birleşik alanına tam olarak eşittir;
- ikinci olarak, üçü de köşegen ile ikiye bölünmüştür. Bu, şunları verir[5]:
Uygulamalar ve genişletmeler

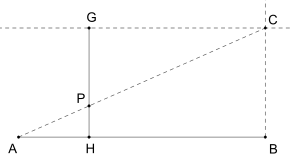
Gnomon teoremi, cetvel ve pergelle yapılan çizimler yöntemiyle belirli bir paralelkenar veya dikdörtgene eşit alana sahip yeni bir paralelkenar veya dikdörtgen oluşturmak için kullanılabilir. Bu aynı zamanda geometrik terimlerle iki sayının bölünmesinin temsil edilmesine izin verir, bu da geometrik problemleri cebirsel terimlerle yeniden formüle etmek için önemli bir özelliktir. Daha kesin olarak, iki sayı doğru parçalarının uzunlukları olarak verilirse, uzunluğu bu iki sayının bölümü olan üçüncü bir doğru parçası oluşturulabilir (şekle bakınız). Diğer bir uygulama, bir doğru parçasının (farklı uzunluktaki) diğer bir doğru parçasına bölme oranının aktarılması, böylece diğer doğru parçasının belirli bir doğru parçası ve bölüntüsüyle aynı oranda bölünmesidir (şekle bakınız).[2]
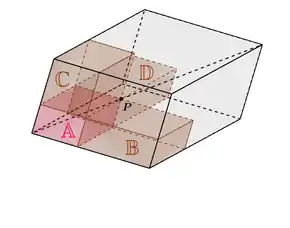
Paralel yüzlüler için benzer bir ifade üç boyutlu olarak yapılabilir. Bu durumda, bir paralel yüzeyin cisim köşegeni üzerinde bir noktası vardır ve iki paralel çizgi yerine noktası boyunca her biri paralel yüzlüye paralel olan üç düzleminiz vardır. Üç düzlem, paralel yüzlüleri sekiz küçük paralel yüzeye böler; bunlardan ikisi köşegeni çevreler ve noktasında buluşur. Şimdi, köşegenin etrafındaki bu iki paralel yüzlüden her biri kendisine bağlı kalan altı paralel yüzlüden üçüne sahiptir, bu üçü tamamlayıcı rolünü oynar ve eşit hacimdedir (şekle bakınız)[3].
İç içe paralelkenarlar hakkında genel teorem
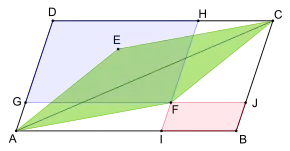
yeşil alan = mavi alan - kırmızı alan
Gnomon teoremi, ortak köşegenli iç içe paralelkenarlar hakkında daha genel bir ifadenin özel bir durumudur. Verilen bir paralelkenar için, köşegen olarak 'yi içeren herhangi bir iç paralelkenarını düşünün. Ayrıca, kenarları dış paralelkenarın kenarlarına paralel olan ve iç paralelkenar ile tepe noktasını paylaşan benzersiz şekilde belirlenmiş iki paralelkenar ve vardır. Şimdi bu iki paralelkenarın alanlarının farkı, iç paralelkenarın alanına eşittir[3], yani:
Bu ifade, köşeleri köşegen üzerinde olan bozulmuş bir iç paralelkenarına bakıldığında gnomon teoremini verir. Bu, özellikle paralelkenarlar ve için, ortak noktaları 'nin köşegen üzerinde olduğu ve alanlarının farkının sıfır olduğu anlamına gelir, bu tam olarak gnomon teoreminin ifade ettiği şeydir.
Tarihsel yönü
Gnomon teoremi, Öklid'in Elemanlarında (MÖ 300 civarında) yer alacak kadar erken tanımlanmış ve diğer teoremlerin türetilmesinde önemli bir rol oynamıştır. Gnomon terimini kullanmadan paralelkenarlar hakkında bir ifade olarak ifade edildiği Elemanların I. kitabında 43 numaralı önerme olarak verilmiştir. İkincisi, Elemanların II. kitabının ikinci tanımı olarak Öklid tarafından tanıtılmıştır. Gnomon ve özelliklerinin önemli bir rol oynadığı diğer teoremler, Kitap II'deki önerme 6, Kitap VI'daki önerme 29 ve Kitap XIII'deki 1'den 4'e kadar olan önermelerdir.[5][6][7]
Notlar
- Gazalé, Midhat J. (1999), Gnomon: From Pharaohs to Fractals, Princeton University Press, ISBN 9780691005140.
- Lorenz Halbeisen, Norbert Hungerbühler, Juan Läuchli: Mit harmonischen Verhältnissen zu Kegelschnitten: Perlen der klassischen Geometrie. Springer 2016, 9783662530344, ss. 190-191
- William J. Hazard: Generalizations of the Theorem of Pythagoras and Euclid's Theorem of the Gnomon. The American Mathematical Monthly, volume 36, no. 1 (Jan., 1929), ss. 32–34 (JSTOR 28 Kasım 2018 tarihinde Wayback Machine sitesinde arşivlendi.)
- Johannes Tropfke: Geschichte der Elementarmathematik Ebene Geometrie – Band 4: Ebene Geometrie. Walter de Gruyter, 2011, 9783111626932, ss. 134-135 26 Ocak 2019 tarihinde Wayback Machine sitesinde arşivlendi. (Almanca)
- Roger Herz-Fischler: A Mathematical History of the Golden Number. Dover, 2013, 9780486152325, ss.35–36 26 Ocak 2019 tarihinde Wayback Machine sitesinde arşivlendi.
- Paolo Vighi, Igino Aschieri: From Art to Mathematics in the Paintings of Theo van Doesburg. In: Vittorio Capecchi, Massimo Buscema, Pierluigi Contucci, Bruno D'Amore (editörler): Applications of Mathematics in Models, Artificial Neural Networks and Arts. Springer, 2010, 9789048185818, ss. 601–610, in particular ss. 603–606
- George W. Evans: Some of Euclid's Algebra. The Mathematics Teacher, Volume 20, no. 3 (Mart, 1927), ss. 127–141 (JSTOR 26 Ocak 2019 tarihinde Wayback Machine sitesinde arşivlendi.)
Kaynakça
- Lorenz Halbeisen, Norbert Hungerbühler, Juan Läuchli: Mit harmonischen Verhältnissen zu Kegelschnitten: Perlen der klassischen Geometrie. Springer 2016, 9783662530344, ss. 190–191 (Almanca)
- George W. Evans: Some of Euclid's Algebra. The Mathematics Teacher, Vol. 20, No. 3 (Mart 1927), ss. 127–141 (JSTOR26 Ocak 2019 tarihinde Wayback Machine sitesinde arşivlendi.)
- William J. Hazard: Generalizations of the Theorem of Pythagoras and Euclid's Theorem of the Gnomon. The American Mathematical Monthly, Vol. 36, No. 1 (Ocak 1929), ss. 32–34 (JSTOR28 Kasım 2018 tarihinde Wayback Machine sitesinde arşivlendi.)
- Paolo Vighi, Igino Aschieri: From Art to Mathematics in the Paintings of Theo van Doesburg. In: Vittorio Capecchi, Massimo Buscema, Pierluigi Contucci, Bruno D'Amore (editörler): Applications of Mathematics in Models, Artificial Neural Networks and Arts. Springer, 2010, 9789048185818, ss. 601–610
Dış bağlantılar
| Wikimedia Commons'ta Gnomons (geometry) ile ilgili ortam dosyaları bulunmaktadır. |
- (İngilizce) Theorem of the gnomon3 Şubat 2020 tarihinde Wayback Machine sitesinde arşivlendi. ve Definition of the gnomon3 Şubat 2020 tarihinde Wayback Machine sitesinde arşivlendi. @ Öklid'in Elementler'i
- Robert Langlands tarafından verilmiş konferans dizisi (Matematikten Sayfalar), (Haziran 2003), YTÜ, Metin29 Kasım 2019 tarihinde Wayback Machine sitesinde arşivlendi.
