Cebir
Cebir (Arapça, "parçaların birleşmesi" ya da "kemik yerleştirme"), sayılar teorisini, geometriyi ve analizi içine alan geniş bir matematik dalıdır. Temel matematik işlemlerinden, çember ve daire alanları bulmaya kadar gider. Temel cebir bilim, mühendislik ve eczacılık gibi birçok alanda kullanılmaktadır. Kuramsal cebir ileri matematiğin ağır ve sadece uzmanlar tarafından çalışılan bir koludur.
Cebirle ilgili ilk çalışmalar Babile kadar uzanır.[1] Yakın doğuda Harezmi ve Ömer Hayyam (1050-1123) gibi isimler tarafından geliştirilmiştir.
Temel cebir bilinmeyen değerleri temsilen harfler kullanmasıyla aritmetikten daha farklıdır.[2] denkleminde bir bilinmeyendir ve in değeri her iki tarafa -2 eklenmesiyle şeklinde bulunabilir. Kütle hız ilişkisinde : ve harfleri bilinmeyen değişkenleri ifade eder ise sabit sayıdır. Cebir birçok matematiksel ifadenin çözümünde yardımcı olur.
Farklı anlamları
Tarihsel açıdan cebirin birçok anlamı vardır, bunun sebebi cebirin anlamsal bolluğu ve çevresindeki anlam değiştiren etkenlerdir. Matematik gibi bir dalda bir kelimenin birden fazla anlamının olması karışıklıklara yol açabilir. Bu yanlış anlamaları engellemek için kelimenin etrafına bazı sözcükler eklenir.
- Tek bir kelime olarak tanımlandığında cebir matematiğin büyük bir kısmını kapsar.
- Yalnız başına tanımlandığı zaman lineer cebir veya temel cebir olarak tanımlanabilir.
Matematiğin bir dalı olarak cebir
Cebirin oluşma dönemi ilk olarak bazı matematiksel sayıları harflerle simgeleyerek başladı. Örneğin bazı üstel fonksiyonlarda: formülündeki harflerine verilebilecek değerler ile in değerleri bulnabilir ancak nın olmaması gerekir. İlerleyen dönemlerde cebir, matemetiğin birçok farklı dallarındada kullanılmaya başlamıştır; vektörler, matrisler ve polinomlar gibi. Daha sonra bu tanımlar cebirsel birimler olarak isimlendirilmiştir ve gruplar, yüzükler ve alanlarda kullanılmıştır. 16. yüzyıl'dan önce matematikçiler; cebirciler ve geometriciler olarak iki gruba ayrılmışlardı. 16. ve 17. yüzyıllar sonucunda matematiğin şu anki haline ulaşmasında cebirin büyük katkısı olmuştur. 19. yüzyıl'ın ortalarında matematiğe yeni konular ve yeni dallar eklenmesine rağmen cebirden her zaman faydalanılmıştır. Şu günlerde cebirin konu yelpazesinden bazı parçalar çıkarılmış olsa da (Mathematics Subject Classification[3] 08-Genel cebir sistemleri, 12-Alan teorisi ve polinomlar, 13-Birleşik cebir, 15-Lineer cebir ve multilineer cebir; matris teorisi, 16-Bağlantılı alan ve halka cebri, 17-Bağlantısız alan ve yüzük cebiri, 18-Kategori teorisi; homolojik cebir, 19-K-teorisi ve 20-Grup teorisi)gibi birçok temel konuyu içerisinde barındırmaktadır.
Etimoloji
Cebir kelimesinin kökeni Hârizmî tarafından yazılmış Ilm al-jabr wa'l-muḳābala arapça kitaptan gelmektedir. Kitabın isminin anlamı zorla yani cebirle bir hesabın yapılması bilimi olarak çevrilebilir. Kelimenin algebra (al-gebra) şeklinde İngilizceye eklenmesi ise ortaçağdaki İspanyol, İtalyan veya latinler sayesinde olmuştur. 12. yüzyıldan başlayarak İtalyanların öncülüğünde Arapça yazılan eserler batı dillerine çevrilmeye başlanmıştır, Harazmi'nin Cebir kitabının da bu dönemde çevrilmiş olması ihtimali yüksektir. Cebir kelimesi İspanyolcada halen acil operasyon, ameliyat olarak kullanılmaktadır daha sonra matematiksel anlamları eklenmiştir.
Tarihi
François Viète in 16. yüzyılın başlarından itibaren yapmış olduğu çalışmalar cebirin temellerini oluşturmuştur. 19. yüzyılın sonlarına kadar cebir genel olarak sadece denklem teorileri barındırıyordu.
Cebirin öntarihi

Cebir ilk olarak Babilliler tarafından matematiksel problemleri çözmek amaçlı kullanılmıştır. Matematikte şu an lineer denklemler veya orta dereceli lineer denklemler kullanarak çözülen problemlerin temellerini Babiller cebiri geliştirerek bulmuşlardır. Eski dönemlerde yaşamış olan çoğu Mısırlı, Çinli ve Yunan matematikçiler problem çözümlerinde geometri kökenli çözüm yollarını tercih ediyorlardı. Yunanlar kendi yarattıkları element matematiğini kullanırlardı ve bu yöntem ile birçok karışık sorunları çözmeyi başarmışlardır ancak bu yöntemleri orta çağ İslamına kadar fark edilememiştir. Plato'nun döneminde birçok Yunan matematikçi ani ve şiddetli bir değişime girmiştir. Yunanlar bu dönemde kendi yarattıkları geometrik çözüm yollarını geliştirerek geometrinin temel kuramlarını kullandılar. O yılların belki de en iyi matematikçilerinden biri olan Diophantus ve aynı zamanda Arithmetica kitabının yazarı, cebirsel ifadelerin matematiksel yollarla çözümleri için birçok formülü geliştiren kişi olmuştur ve ilerleyen zamanlarda sayı teorisinin ve kendi yarattığı Diophantus denklemlerinin çıkmasını sağlamıştır. Matematiğin geliştiği ilk dönemlerde Harizmi (d. 780–ö. 850) nin yazdığı The Compendious Book on Calculation by Completion and Balancing isimli kitabı matematikte bazı görüşlerin oluşmasına neden oluyordu çünkü cebirin ve matematiğin temel disiplin kurallarının geometri ve aritmetikten farklı olduğunu söylemiştir. Helenistik matematikçiler Diophantus ve Alexandria ve Hindistanlı matematikçi Brahmagupta, Mısır ve Babillilerin yaratmış olduğu matematik kurallarını devam ettirdiler ve üzerlerine bir şeyler eklemek için çabaladılar. Yazmış oldukları kitaplardanda faydanalarak ilk kez içerisinde sıfır ve eksi sayıların olduğu denklemleri çözmeyi başardılar. Denklemler teorisine göre incelenen cebirin en önemli iki ismi Diophantus ve al-Khwarizmi'nin çalışmaları yıllarca incelenmiştir. Genellikle cebirin babası olarak Diophantus bilinir ancak Harizmi'nin al-jabr disiplin kuralları sonucunda bu unvana onun sahip olması istenmektedir. Diophantus'u destekleyen kişiler Al-Jabr deki cebirin biraz daha elementsel olduğunu ifade etmişlerdir kendi savundukları Arithmetica ve Arithmetica kitaplarının Al-Jabr 'dan daha teorisel olduğunu söylemişlerdir. Al-Khwarizmi yi destekleyenler ise "çıkarma" ve "dengeleme" (toplamanın tersi ve elemanların birbirlerini sıfırlaması) al-jabr kitabının cebiri her şeyden ayrı tutup yeni teoriler üzerine kurulmuş olmasından dolayı sevmişlerdir,[4]. İranlı matematikçi Ömer Hayyam cebirsel geometrik çözümler ve küplü denklemler üzerinde çalışmış biridir. Bir diğer İranlı matematikçi ise Şerafeddin el-Tusî'dir. O da fonksiyonların gelişiminde etkili biri olmuştur. Hint matematikçiler Mahavira ve II. Bhaskara, İranlı matematikçi Al-Karaji,[5] ve Çinli matematikçi Zhu Shijie birçok küplü denklemin çözümünde etkili olmuşlardır.
Cebirin tarihi
1545'te İtalyan matematikçi Girolamo Cardano Ars magna -Muhteşem sanat isimli kitabını yayınladı, 40 bölümlük harika bir sanat eseri ve ilk defa küplü ve üstlü denklemleri anlatılmıştır. François Viète'nin 16. yüzyılın sonlarına doğru yapmış olduğu çalışmalar cebirin klasik disiplin temellernin atılmasını sağlamıştır. 1637 yılında René Descartes, La Géométrie isimli kitabını yayınlamıştır ve analitik geometrinin ilk temelleri atılmıştır. Bir diğer önemli gelişmelerden biri ise 16. yüzyılın ortalarına doğru köklü ve küplü denklemlerin çözülmesidir. Determinant formülü Japon matematikçi Kowa Seki tarafından 17. yüzyılda bulunmuştur ve buna takiben Gottfried Leibniz 10 sene sonra lineer denklemlerin çözümünü kolaylaştırma adına matris'i yaratmıştır. Soyut cebir 19. yüzyılda geliştirilmiştir, şu anda Galois theory olarak bilinen denklemleri çözebilmek için geliştirilmişlerdir. "Modern algebra" 19. yüzyıla kökleri dayanan önemli bir konudur örneğin, Richard Dedekind ve Leopold Kronecker,cebirsel sayı teorisi ve cebirsel geometri'yi yarattığı kabul edilen ve kullanan kişilerdir.
'Cebir' kelimesini barındıran konular
Matematiğin alanları,
- Temel cebir, okullarda gösterilen cebirsel denklemler
- Soyut cebir, gruplar,halkalar ve cisim gibi cebirsel yapıların incelendiği alan
- Lineer cebir, lineer denklemlerin, vektör uzaylarının ve matrislerin kullanıldığı cebir
- Komütatif cebir, değişmeli halkaların incelendiği alan
- Bilgisayar cebiri, bilgisayar program yazılımlarında kullanılan cebir
- Homolojik cebir, topolojik katman çözümlerinde kullanılan cebir
- Evrensel cebir, her cebirsel özelliğin incelendiği cebir
- Cebirsel sayı teorisi, sayı ve rakamların cebirsel bir yönle araştırılması
- Cebirsel geometri, eğik şekillerin hacim ve alan hesaplamalarında
- Cebirsel kombinatorik, cebirsel metodların kombinatorik sorularına uygulandığı alan
Birçok matematiksel terim cebir olarak tanımlanır;
- Bir cisim üzerindeki cebir .
Halka ve cisim üzerine tanımlanan birçok cebirin özel ismi vardır :- Bağlı cebir
- Bağımsız cebir
- Lie cebiri
- Hopf cebiri
- C*-cebiri
- Simetrik cebir
- Dış cebir
- Tensör cebiri
- Hesaplama teorisinde,
- Sigma-cebiri
- Bir grup üzerindeki cebir
- Kategori teorisi
- F-cebiri ve F-co cebiri
- T-algebra
- Mantıkta,
- İlişkisel cebir,
- Boole cebiri,
- Heyting cebiri
İlkokul cebiri
İlkokul cebiri genellikle sadece aritmetik bilgisi olan öğrencilere cebirin temel kurallarını öğretmek amaçlı gösterilen bir cebir türüdür.En temel ve basit cebir türüdür. Aritmetikte sadece sayılar ve aritmetiksel işlemler(+, −, ×, ÷) kullanılır. Cebirde ise sayılar genellikle değişken kabul edilir ve harflerle ifade edilir (a, n, x, y ya da z) gibi.
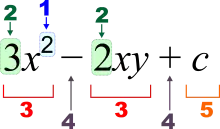
1 – Üst
2 – katsayı
3 – terim
4 – işlem
5 – sabit teri
x y – değişkenler c – sabit sayı
- Temel cebir kurallarının kullanılması ile basit bir bilinmeyenli denklemlerin çözüm şekilleri anlatılır, sayı çeşitleri doğal sayılar,ardışık sayılar gibi sayı türleri anlatılır ve basit fonksiyonların özellikleri tanımlanır.
Polinomlar
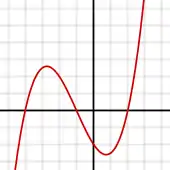
ax2 + bx + c biçimindeki fonksiyonların x değerlerinin sıfır olduğu noktalarda çözüm kümesi bulunması denklemleridir. Her denklemin derecesine bağlı olarak kök türleri ve kök sayıları değişme gösterir. Fonksiyon ve polinomlar birbirlerine bağlı birimlerdir ve matematik ile cebirin önemli ve ileriye bağlı konularının temellerini oluşturan ciddi konulardır.
Cebirin öğretilmesi
Temel, basit cebirin genellikle on bir yaşına gelmiş olan çocuklara anlatılması tercih edilir. Amerika'da genellikle sekizinci sınıfta temel cebir öğretimi başlar. 1997'den beri Virginya Üniversitesi gibi birçok üniversite bilgisayar yardımlı ve küçük gruplar halinde gençlere temel cebir eğitimi vermektedir.
Soyut cebir
Soyut cebir genellikle aritmetik ve sayı teorilerinin birleşimini ifade eden bir cebir türüdür; Setler:Sayı türlerini incelemekten ziyade soyut cebir matematiğin tüm birimlerini bir çatı altında inceler ve tüm bu setler matrisler ve üstlü denklemler içerebilir bunlara ikinci veya üçüncü dereceden polinomların incelenmeside dahildir.
Denklemler arası işlemler: + ve - işlemlerinin yanı sıra * ve / işlemleri cebirin temel işlemlerindendir ve her denklem veya fonksiyon,polinom için çözülebilmeleri için gerekli tanım araşlıkları ve çözüm kümelerinin bulunduğu alanlar sorularda önceden ayarlanmış ve bildirilmiş olmalıdır.
Etkisiz eleman: Bir denklemde sonucu yapılan işleme göre değiştirmeyen veya aynı tutan elemanlara etkisiz eleman denir. Yapılacak matematiksel işlemin türüne göre etkisiz elemanlar değişkenlik gösterir örneğin bir çarpma işleminde etkisiz eleman bir iken, bir toplama işleminde bu eleman sıfırdır.
Ters elemanlar: Ters elemanlar bir sayının bölüm halinde yazılması ile oluşurlar a ∗ a−1 = 1 ve a−1 ∗ a = 1 gibi.
Dağılma özelliği: Matematiksel bir işlemde toplam veya çarpım halindeki elemanların grup halinde yerlerinin değiştirilmesi sonuçta bir değişikliğe neden olmaz. (2 + 3) + 4 = 2 + (3 + 4) genel olarak (a ∗ b) ∗ c = a ∗ (b ∗ c) ifade edilebilir.
Değişken özelliği: Toplamda veya çarpma işlemlerinde elemanların yerlerinin değiştirilmesi sonucu etkilemez ve buna cebirin değişme özelliği denir. 2 + 3 = 3 + 2 ve a ∗ b = b ∗ a
Gruplar
Gruplar genel olarak bir tanım aralığındaki setler ve bir çarpım işlemi olarak tanımlanır ve sonuç olarak:
- e ∗ a işlemleri S setindeki bir çözüm elemanına eşit çıkar
- S tanım aralığındaki her elemanın bir tersi vardır a ∗ a−1 ve a−1 ∗ a
- Eğer a, b ve c , S 'in elemanları ise (a ∗ b) ∗ c işlemi a ∗ (b ∗ c) işlemine eşittir. Bir grup içerisindeki işlemler birbirlerini sıfırladıkları zaman eşitlik söz konuus olur ve türlü şekillerde ifade edilebilirler (a + b) + c = a + (b + c). Rasyonel sayılarda bir(1) eleamanı çarpım işlemlerinde etkisiz eleman görevi görür 1 × a = a × 1 = a ve a is 1/a çünkü a × 1/a = 1.
| Examples | ||||||||||
| Set: | Doğal Sayılar N | Aralıklar Z | Rasyonel sayılar Q (also real R and complex C numbers) | Integers modulo 3: Z3 = {0, 1, 2} | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Çarpım | + | × (w/o sıfır) | + | × (w/o sıfır) | + | − | × (w/o sıfır) | ÷ (w/o sıfır) | + | × (w/o sıfır) |
| Kapalı | Evet | Evet | Evet | Evet | Evet | Evet | Evet | Evet | Evet | Evet |
| Etkisiz | 0 | 1 | 0 | 1 | 0 | N/A | 1 | N/A | 0 | 1 |
| Tersi | N/A | N/A | −a | N/A | −a | N/A | 1/a | N/A | 0, 2, 1, respectively | N/A, 1, 2, respectively |
| Dağılma özelliği | Evet | Evet | Evet | Evet | Evet | Hayır | Evet | Hayır | Evet | Evet |
| Değişme özelliği | Evet | Evet | Evet | Evet | Evet | Hayır | Evet | Hayır | Evet | Evet |
| Structure | monoid | monoid | abelian group | monoid | abelian group | quasigroup | abelian group | quasigroup | abelian group | abelian group (Z2) |
Cebirsel Alanlar
Cebirsel işlemlerde gruplar arasında genellikle tek işlem bulunur en azından basit cebir kurallarına göre böyle kabul edilir. Detayı incelendiği zaman cebirsel alan ve yüzük önemli bir hale gelir.
Bir yüzük matematiğinin iki temel işlemi vardır (+) ve (×), × , + işlem sıraına göre daha öndedir. İlk işlem (+) sonucunda bir abelian grubu oluşur. İkinci işlem sonucunda (×) dağılma özelliği ile işleme etki eder, ancak bu işlemler oluşurken herhangi bir şekilde bir kesir işlemini tanımsız duruma getirme veya fonksiyon tersi alınmasına ihtiyaç duyulmadğı için cebirsel sistemde bir sorun oluşmamaktadır. Toplam işlemlerinin (+) etkisiz elemanı 0 olarak kabul edilir ve toplam işlemlerini tersi a, −a olarak yazılabilir.
Dağılma özelliğinde (a + b) × c = a × c + b × c ve c × (a + b) = c × a + c × b, eşit olduğu için cebirsel sistemde çarpımın dağılma özelliği kullanılmış olmuştur.
Dipnotlar
- Struik, Dirk J. (1987). A Concise History of Mathematics. New York: Dover Publications. ISBN 978-0-486-60255-4.
- Boyer 1991, Europe in the Middle Ages, s. 258
- "2010 Mathematics Subject Classification". 6 Haziran 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 12 Haziran 2014.
- Boyer 1991, "The Arabic" p. 229
- Boyer 1991, "The Arabic Hegemony" p. 239 "Abu'l Wefa başarılı bir cebir ustası aynı zamanda geoemetricidir. ... Onu eğiten al-Karkhi sonuç olarak Diophantusun en büyük destekçilerinden biri haline geldi ancak onun teorilerinin aynılarını kullanmazdı! ... al-Karkhi ilk sayısal denklemlerin ve pozitif köklü sonuçların oluşmasını sağlayan kişi olmuştur. ax2n + bxn = c (sadece pozitif köklü denklemler),"
Kaynakça
- Boyer, Carl B. (1991), A History of Mathematics (Second Edition bas.), John Wiley & Sons, Inc., ISBN 0-471-54397-7
- Donald R. Hill, Islamic Science and Engineering (Edinburgh University Press, 1994).
- Ziauddin Sardar, Jerry Ravetz, and Borin Van Loon, Introducing Mathematics (Totem Books, 1999).
- George Gheverghese Joseph, The Crest of the Peacock: Non-European Roots of Mathematics (Penguin Books, 2000).
- John J O'Connor and Edmund F Robertson, History Topics: Algebra Index3 Mart 2016 tarihinde Wayback Machine sitesinde arşivlendi.. In MacTutor History of Mathematics archive (University of St Andrews, 2005).
- I.N. Herstein: Topics in Algebra. ISBN 0-471-02371-X
- R.B.J.T. Allenby: Rings, Fields and Groups. ISBN 0-340-54440-6
- L. Euler: Elements of Algebra, ISBN 978-1-899618-73-6
- Asimov, Isaac (1961). Realm of Algebra. Houghton Mifflin.
