Manyetik tek kutup
Manyetik monopol (veya manyetik tek kutuplu veya manyetik tek kutup), parçacık fiziğinde yalıtılmış tek bir manyetik kutbu olan (sadece manyetik kuzey veya manyetik güney kutuplarına sahip) kuramsal bir temel parçacıktır.[1] Daha teknik terimlerle açıklanacak olursa, bir manyetik monopol net manyetik yükü olan bir parçacıktır. Bu teori köklerini manyetik monopollerin varlığını öngören parçacık teorileri, özellikle büyük birleşim (Grand Unifying) ve süper sicim teorilerinden alır. Çubuk şeklindeki mıknatısların manyetik alanı ve elektromanyetikler manyetik monopollerden kaynaklanmazlar. Manyetik monopollerin varlığını kanıtlayan herhangi bir deneysel veri yoktur. Bazı yoğun madde sistemleri efektif manyetik monopol, quasi parçacığını veya matematiksel olarak manyetik monopollerle benzeşen bazı fenomenleri barındırır.
Tarihsel gelişimi
20. yüzyıl öncesi
Birçok eski bilim insanı mıknatıs taşının manyetizmasını elektrik yüküne benzer şekilde birbirini çeken veya iten iki farklı manyetik sıvıya, kuzey kutup sıvısı bir tarafta ve güney kutup sıvısı diğer tarafta, bağlıyordu. Fakat 19. yüzyılda elektromanyetizmanın daha iyi anlaşılması mıknatıs taşının manyetik özelliklerinin manyetik monopol sıvılarla değil, Ampere yasası ile düzgün bir şekilde açıklandığını gösterdi. Gauss yasası, Maxwell'in denklemlerinden biri manyetik monopollerin var olmadığını açıklayan matematiksel ifadelerdir. Yine de Pierre Curie, 1849 yılında manyetik monopollerin makul bir biçimde var olabileceğini ifade etti, şimdiye kadar olmamasına rağmen.
20. yüzyıl
Manyetik yükün kuantum teorisi fizikçi Paul A.M. Dirac tarafından 1931 yılında yazılan bir çalışma ile başladı. Bu çaılşmada Dirac, eğer evrende bir manyetik monopol var ise evrendeki bütün elektrik yüklerinin kuantize olması gerektiğini belirtti(Dirac kuantizasyon kuşulu)[1]. Gerçektende elektrik yükü manyetik monopolün varlığı ile (henüz kanıtlanmamıştır) tutarlı bir biçimde kuantizedir.
Dirac'ın bu çalışmasından beri birçok sistematik monopol arayışı gerçekleştirilmiştir. 1975 ve 1982 yıllarındaki deneyler, manyetik monopol varlığına aday kimi sonuçlar doğursa da günümüzde sonuçsuz olarak kabul edilir. Yani manyetik monopolün var olup olmadığı hala cevabı belirsiz bir sorudur. Teorik parçacık fiziğindeki ileri gelişmeler, özellikle kuantum kütleçekimi ve büyük birleşim kuramındaki gelişmeler, monopolün var olduğuna dair daha zorlayıcı argümanlar (aşağıda detaylandırılmıştır) doğmasına sebep olmuştur. Joseph Polchinski, bir sicim teorisyeni, manyetik monopollerin varlığını “ fizik hakkında henüz görülmemiş konular arasında girilebilecek en güvenli iddia” şeklinde yorumlamıştır.
Bütün bu teoriler deneylerle tutarsız olmak zorunda değildir. Kimi teorik modellerde, manyetik monopollerin gözlenmesi pek mümkün değildir çünkü parçacık hızlandırıcılarda üretilemeyecek kadar ağırdır ve ayrıca evrende çok ender rastlandıklarından parçacık detektörlerince algılanması çok düşük bir ihtimaldir.
Bazı yoğunlaşmış madde sistemleri yüzeysel olarak manyetik monopollere benzeyen akı tüpü olarak adlandırılan bir yapı önerirler. Bu akı tüpünün uçları bir manyetik monopol gibi davranır ama bu birbirinden bağımsız hareket ettikleri için yine birbirinden bağımsız manyetik monopol quasi-parçacığı gibi de düşünülebilirler.2009 yılından bu yana popüle medya dan birçok haberde yanlış bir biçimde manyetik monopollerin keşfi gibi lanse edilse de iki fenomen birbiriyle ancak yüzeysel olarak bağlı olabilir. Bu yoğunlaşmış madde sistemleri açık bir araştırma alanı olarak devam etmektedir(yoğunlaşmış madde sistemlerinde manyetik monopoller kısmına bakınız).
Sıradan maddelerde kutuplar ve manyetizma
Bugüne kadar izole edilmiş bütün maddeler periyodik cetveldeki tüm atomlar ve standart modeldeki tüm parçacıklar dahil olmak üzere sıfır manyetik monopole yüküne sahipti. Böylelikle, manyetizma ve manyetiklerin olağan fenomenleri manyeetic monopoller ile bir alakası yoktur.
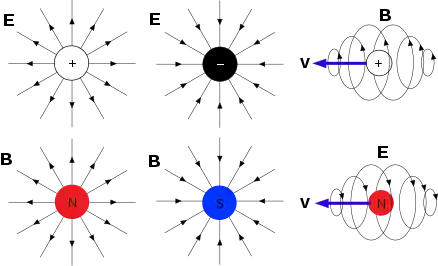
Bunun yerine, sıradan maddelerin manyetik özelliğini iki sebebten kaynaklanır. İlk olarak Ampere yasasına göre elektrik akımı manyetik alan yaratır. İkinci olarak, birçok elementer parçacık “gerçek” bir manyetik momente sahiptir, ki en önemlisi elektron manyetik dipol momentidir. (Bu manyetizma kuantum-mekaniksel "spin" ile ilintilidir.) Matematiksel olarak, bir objenin manyetik alanı sıklıkla çok-kutuplu(multipol) açılımı ile açıklanır. Bu manyetik alanı bileşke alanların toplamı şeklinde kimi matematiksel formlar kullanılarak yapılan bir açıklamadır. çok-kutuplu açılımın ilk terimi monopol dür, ikinci terimi dipoldür, sonra quadropol, oktapol şeklinde devam eder. Örneğin bu terimlerin herhangi biri elektrik alan multipol açılımında kullnılabilir. Fakat, manyetik alanın multipol açılımında “monopol” terimi tam olarak sıfırdır(sıradan bir madde için). Bir manyetik monopol eğer gerçekten var ise monopol terimi sıfırdan farklı olan bir manyetik alanı tanımlayan özelliğe sahip olmalıdır.
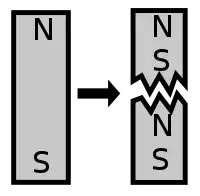
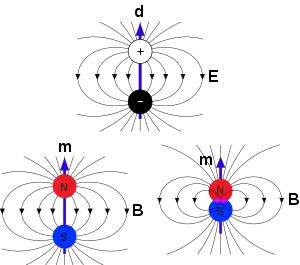
Bir manyetik dipol, ağırlıklı olarak multipol açılımındaki manyetik dipol ile açıklanır. “Dipol” terimi “iki-kutuplu” manasına gelir ve bu iki kutup bir tarafta kuzey ve diğer tarafı güney şeklinde isimlendirilir. Bu durum bir tarafı pozitif diğer tarafı negatif yükten oluşan elektrik dipole çok benzer. Fakat elektrik dipol ile manyetik dipol oldukça farklıdır. Sıradan bir madde tarafından oluşturulan elektrik dipolde pozitif yük protondan negatif yük ise elektron tarafından oluşturulur ama manyetik dipolün kutupları farklı iki maddeden oluşmaz. Bunun yerine manyetik monopolün kutupları bütün elektrik akımlarının toplam efekti ve manyetik boyunca var olan gerçek momentlerden meydana gelir. Bu sebepten ötürü manyetik dipolün iki kutbu daima ters işaretli ve eşit büyüklükte kuvvete sahiptir ve ayrıca bu iki kutup asla birbirinden ayrılamaz.
Maxwell denklemleri
Maxwellin elektromanyetik denklemleri elektrik ve manyetik alanı birbiri ile ilişkilendirir ve elektrik yüklerinin hareketini açıklar. Bu denklemler elektrik yüklerini açıklar fakat manyetik yükleri varsaymaz. Fakat bu duruma bir istisna vardır oda denklemlerin elektrik ve manyetik alaların değişimi altında simetrik özellikler sahip olmasıdır. Simetrik Maxwell denklemeleri bütün yükler sıfıra eşit olduğunda yazılabilir ve aslında elektromanyetik dalga fonksiyonu bu şekilde türetilir.
Tamamen simetrik Maxwell denklemleri eğer elektrik yüküne benzer şekilde manyetik yük kavramına da izin verilirse yeniden yazılabilir. Bu sayede manyetik yük yoğunluğu kavramı,ρm, ile birlikte manyetik akım yoğunluğu,jm, kavramı da denklemlerde yer alabilir.
Eğer manyetik yükler yok ise, veya var fakat uzayın herhangi bir yerinde bulunmuyor ise, Maxwell denklemlerinin yeni terimlerinin hepsi sıfıra eşit olur ve genişletilmiş denklemler elektromanyetik denklemlerin geleneksel olan ∇⋅B = 0 haline indirgenir (Burada ∇⋅) diverjans ve B ise manyetik alandır).
Gauss cgs birimleri
Gaus cgs birim sisteminde genişletilmiş Maxwell denklemleri aşağıdaki gibidir.
Manyetik monopollerle Maxwell denklemleri ve Lorentz kuvvet denklemi (Birimler: Gaussian cgs) Name Manyetik monopol olmadan Manyetik monopol durumunda Gauss Yasası Manyetizma için Gauss Yasası Faraday İndüklenme Yasası Ampère Yasası (Maxwell denk. birlikte) Lorentz kuvvet denklemi [4][5]
Bu denklemlerde ρm manyetik yük yoğunluğunu, jm manyetik akım yoğunluğunu ve qm test parçacığının manyetik yükünü temsil eder. Diğer başka tanımlar ve detaylar için Maxwell denklemleri sayfasına bakınız. Ayrıca denklemlerin birimsiz türlerini elde etmek için c çarpanlarını siliniz.
SI'ya göre
SI birimlerinde, manyetik yük için iki çelişen birim vardır;qm: webers (Wb) ve amper·meters (A·m). İkisinin birbir arasında dönşümü;qm(Wb) = μ0qm(A·m) şeklindedir çünkü birimlerin 1 Wb = 1 H·A = (1 H·m-1)·(1 A·m) olduğu birimsel analiz ile görülür. (H:henry – SI birim sistemindeinductance birimidir). Bundan sonra Maxwell denklemleri aşağıdaki formu alır:
Manyetik monopollerle Maxwell denklemleri ve Lorentz kuvvet denklemi (Birimler: SI) Yasa Manyetik monopol olmadan Weber konvensiyonu Amper·metre konvensiyonu Gauss Yasası Manyetizma için Gauss Yasası Faraday İndüklenme Yasası Ampère Yasası (Maxwell denk. birlikte) Lorentz kuvvet denklemi
Tensör formülasyonu
Maxwell denklemleri tensor ler ile birlikte Lorentz koveransını daha anlaşılır hale getirir. Genel olarak denklemler şu şekildedir:
Maxwell denklemleri Gaussian birimlerde SI (Wb) SI (A⋅m) Faraday-Gauss yasası Ampère-Gauss yasası Lorentz kuvvet yasası
Bu denklemlerde
- Fαβ elektromanyetik tensörü , αβ = 12εαβγδFγδ ifadesi ikili elektromanyetik tensörü.
- qe elektrik yüküne ve qm manyetik yüküne sahip bir parçacık için; v dört-hız ve p dört-momentumu;
- verilen bir elektrik ve manyetik alan dağılımı için Je = (ρe, je) dört-akımı ve Jm = (ρm, jm) dört manyetik akımı
temsil eder.
Sadece elektrik yüküne sahip bir parçacığın alanı klasik elektromanyetizmanın kovaryant formülasyonuna göre dört-potansiyel kullanılarak açıklanabilir.
Fakat, bu förmül hem elektrik hem de manyetik yüke sahip bir parçacık için yetersiz kalır ve potansiyel içeren bir başka $P$ terimi ekleriz P:
Alanların bu formülü, Shanmugadhasan daha önce öne sürmesine rağmen sıklıkla Cabibo-Ferrari ilişkisi olarak anılır. Burada εαβγδ ifadesi Levi-Civita sembolü olarak isimlendirilir ve endeksleri de Einstein toplam düzenine göre hareket eder
İkililik dönüşümü
Genelleştirilmiş Maxwell denklemleri ikililik dönüşümü olarak adlandırılan kesin bir simetriye sahiptir. İstenirse herhangi bir gerçek ξ açısı seçilebilir ve aynı anda alanları ve evrendeki bütün yükleri aşağıdaki gibi değiştirir:
Yükler ve Akımlar Alanlar
“x üssü” şeklindeki ifadeler dönüşümden önceki alanlar ve yüklerdir ve üssü olmayan ifadeler dönüşümden sonrasını içindir. Alanlar ve yükler değişimden sonra da aynı Maxwell denklemlerine uyar. Kullanılan matris iki boyutlu dönüşüm matrisidir.
Dönüşümün ikililiğinden dolayı parçacığın sadece manyetik yüke mi yoksa sadece elektrik yüke mi ya da her ikisine birden mi sahip olduğu sadece parçacığın davranışından ve Maxwell denklemleriniyle karşılaştırmak suretiyle anlaşılamaz.Örneğin,bu sadece bir düzendir Maxwell denklemlerinin gerekliliği değil, öyle ki elektronlar elektronlar elektrik yüküne sahip fakat manyetik yüke sahip değildir ve bir ξ = π/2 dönüşümünden sonra diğer şekilde tezahür eder. Önemli olan deneysel gerçek şudur ki şu ana kadar gözlenen bütün parçacıklar aynı manyetik yük bölü elektrik yük oranına sahiptir. İkililik dönşümleri bu oranı herhangi bir keyfi sayı ile değiştirebilir fakat bütün parçacıkların aynı orana sahip olduğu gerçeğini değiştiremez. Bu durumda olduğundan, bir ikilik dönüşüm sıfır olması için bu oran ayarlar yapılabilir ve bu sayede bütün parçacıklar sıfır manyetik yüke sahip olabilir. Bu seçim geleneksel elektrik ve manyetizma tanımının altını çizer.
Dirac kuantizasyonu
Kuantum teorisini tanımlayan gelişmelerden biri de Paul Dirac'ın rölativistik kuantu elektromanyetizma hakkındaki çalışmalarıdır. Onun formüllerinden önce elektrik yüklerinin varlığı basit bir şekilde kuantum mekaniğinin denklemlerine eklendi,fakat, 1931 yılında Dirac gösterdi ki soyu bir elektrik yükü doğal olarak kuantum mekaniğinden “dışarıya düşer”. Yani başka bir deyişle manyetik yüke sahip olsak bile Maxwell denklemleri sahip olduğu formu koruyabilir. Durgun bir elektrik monopol (elektron gibi) ve durgun bir manyetik monopole sahip bir sistem düşünün. Klasik olarak baktığımızda bu sistemin etrafını saran bir momentum yoğunluğu vardır (Poynting vektörü ile verilen) ve aynı zamanda qeqm, çarpımına doğrusal, birbirleri arası mesafeden bağımsız bir toplam açısal momentum a sahiptir. Fakat, kuantum mekaniğinin “diktesine” göre açısal momentum ħ birimlerince kuantize olur yani yukardaki çarpımda kuantize olur. Bu demektir ki eğer evrende tek bir manyetik monopol var ise ve Maxwell denklemlerini formunu koruyorsa bütün elektrik yüklerinin kuantize olması gerekir. Kuantize olmuş bir manyetik yükün birimi nedir? Yukarıdaki örnekte toplam açısal momentumu bütün uzay boyunca integral alarak bulabiliyor olsakta, Dirac farklı bir şekilde yaklaştı ve bu sayede yeni fikirlere ulaştı. Dirac, aslında bulunan, manyetik alanı qm / r 2 şeklinde radyal uzanan bir nokta şeklinde manyetik bir yük düşündü. B nin diverjansının hemen hemen her yerde sıfır olmasından dolayı,r=0 da manyetik monopol mahalin haricinde, potensiyelinin vektör potensiyeli manyetik alana eşit olan bir manyetik alan tanımlanabilir.
Fakat, vektör potansiyeli, küresel olarak kesin bir şekilde tanımlanamaz çünkü manyetik alan orijindeki Dirac delta fonksiyonu ile orantılıdır. Kuzey yarımküredeki (yarım uzay z > 0 üstünde kalan) vektör potansiyeli için bir fonksiyon kümesi ve güney yarımküredeki vektör potansiyelleri için yine ayrı bir fonksiypn kümesi tanımlamamız gerekir. Bu iki vektör fonksiyonu “ekvatorda” birleşir (parçacığı içeren z = 0 düzlemi) ve gösterge dönüşümünce ayrılırlar. ”Ekvatorda” bir yörüngede olan elektriksel olarak yüklenmiş bir parçacığın (“probe yükü”) Dalga fonksiyonu genellikle bir faz ile değişir, tıpkı Aharonov–Bohm efekti gibi. Bu faz elektrik yükü qe ile ve kaynağın manyetik yükü qm ile doğru orantılıdır. Dirac, dalga fonksiyonu Dirac denklemi ile açıklanan bir elektron düşünmüştü.
Bir tam tur sonunda elektron yörüngede aynı noktaya döndüğünden, dalga fonksiyonunun eiφ fazı φ değişmemelidir, ki bu dalga fonksiyonunna eklenen bir φ fazının 2πnin bir katı olması gerektiğini gösterir;
burada ε0 boşluk geçirgenliğini, ħ = h/2π indirgenmiş Planck sabitini, c ışık hızını ve Z ise tam sayılar kümesini ifade eder. Bu “Dirac kuantizasyonu” olarak bilinir. Manyetik monopolün varsayımsal varlığı elektrik yükünün belirli birimleri ile kuantize olduğunu ifade eder ve ayrıca elektrik yükünün varlığı vaarsayımsal manyetik monopolün manyetik yükünün , eğer varlğı kesin ise, elementer elektrik yüküne ters orantılı birimler ile kuantize olduğunu ifade eder.
Vakti zamanında böyle bir şeyin var olduğu fikri hatta gerekli olup olmadığı dahi kesin değildi. Daha sonraları monopole ihtiyaç duyulmaksızın yük kuantizasyonunun açıklayan bir teori çıkageldi. Yani manyetik monopol konsepti merak edilmeye devam etti. Fakat, bu yeni ufuklar açan çalışmadan dolayı yük kuantizasyonun kabul edilen başka bir açıklaması olmadı. (Yerel ölçünün değişmezliği kavramı -aşağıdaki ölçü teorisine baknınız- yük kuantizasyonu için monopol fikrinin yardımı olmadan doğal bir açıklama getirir fakat U(1) ölçü grubu kompakt ise; diğer durumlarda yine de manyetik monopole ihtiyaç duyarız ).
Eğer güney yarıküre için vektör potansiyeli kavramının tanımını uzatırsak, orijinden başlayıp kuzey yarıküre yönünde uzanan yarı-sonsuz doğru haricinde her yerde kuantizasyon tanımlı olacaktır. Bu yarı-sonsuz doğru Dirac sicimi olarak tanımlanır ve doğrunun dalga fonksiyonuna etkisi Aharonov–Bohm efektindeki selenodi etkisine çok benzerdir. Dirac sicimi etrafındaki fazların değersiz oluşundan dolayı kuantizasyon koşulu var olur; ki bu da Dirac siciminin fiziksel olmayana bir şey olduğunun gösterir. Dirac sicimi kullanılan kordinat sisteminin ancak bir ürünüdür ve ciddi olarak düşünülmesi gerekilmez.
Dirac monopolü Maxwell denkleminin eşsiz bir çözümüdür; (çünkü dünyaçizgisinin uzay-zamandan silinmesini gerektirir) daha karmaşık teorilerde, Hooft–Polyakov monopolü gibi daha hassas çözümler ile “ayağı kaydırılabilir”.
Topolijik yorum
Dirac sicimi
Elektromanyetizma teorisi benzeri bir ölçü teorisi ölçü alanı ile tanımlanır ve bu alanlar uzay-zamandaki her yol için bir grup elemanı ile iştirak eder. Bir sonsuz küçük bir yol için grup elemanı 1 + iAμdxμ olur ki bu da sonlu ve s tarafından parametrize edilmiş bir grup elemanı;
Bu yollardan grup elemanına çizilen harita Wilson dögüsü veya holonomy olarak adlandırılır, ve U(1) ölçü grubu için bu yolu geçerken hangi bir yüklü parçacığın dalga fonksiyonu kazanır
Bir döngü için;
Fakat eğer tüm parçacık yükleri tam sayı e katları ise, akısı 2π/e olan selonid girişim saçaklarına sahip olmaz çünkü faz faktörü bütün yüklü parçacıklar için e2πi = 1 olur. Böyle bir selenoid eğer yeterince ince ise kuantum-mekaniksel olarak görünmezdir. Eğer böyle bir selenoid 2π/e kadar bir akı taşayacak olursa ve eğer bu akı selenoidin herhangi bir ucundan taşacak olursa monopolden ayır edilmez hale gelecektir.
Aslında Dirac’in monopol çözümü çizgi şeklinde sonsuz küçük olan ve bir noktada biten bir selenoid tanımlar ve bu selenoid çözümün özel bir parçasıdır; Dirac sicimi. Dirac sicimi monopol ile karşı manyetik yüklü antimonopolle arasında bir bağlantı kurar, Dirac versiyonunda sicim sonsuza gitmesine rağmen. Sicim gözlemlenemezdir yani istenilen bir yerde konumlandırılabilir, ve iki kordinat eklentisi kullanarak sicimi görülemeyeceği yere kaydırarak eklentilerdeki alanlar tekil olmayan bir hale getirilebilir.
Büyük birleştirilmiş teoriler
U(1) ölçü grubu olduğu durum özel bir durumdur çünkü bütün indirgenemez temsilleri aynı boyuttadır; yük bir tam sayı mıktarınca daha büyüktür -lakin alan hala bir karmaşık sayıdır- ki bu sayede U(1) ölçü grubu teorisinde limiti çelişki almak mümkün olur. Yükün kuantumu küçük hale gelir fakat bütün yüklü parçacıklar çok büyük bir yük kuantasına sahip olur yani yükü sonsuz olarak kalır. Kompakt olmayan bir U(1) ölçü grubu teorisinde parçacıkların yükleri genellikle tek bir birimin bir tam sayı katı şeklinde değildir. Yük kuantizasyonu deneysel olarak bir kesinlik olabileceği için electromanyetizmanın U(1) ölçü grubu teorisinin kompakt olduğu açıktır.
Büyük birleştirilmiş teoriler (BBT) kompakt U(1) gurublarına delalet eder, yani aslında mantıksal olarak manyetik monopol kavramından bağımsız bir yol lie yük kuantizasyonunu açıklarlar. Fakat, açılama esasen aynıdır çünkü herhangi bir uzak mesafelerde U(1) ölçü grubuna ayrılan BBT’de manyetik monopol içerir.
Bu iddia topolojiktir;
- Bir ölçü alan holonomi göstergesi grubunun elemanları döngüler eşler. Sonsuz döngüler kimliğine sonsuz yakın grup elemanları eşleştirilir.
- Eğer uzayda büyük bir küreyi hayal ederseniz, kuzey kutbunda başlayan ve biten bir sonsuz döngü deforme olabilir.
- yakalamak döngüler bir sekansdır, yani holonomisine elemanları, gösterge grubu bir hat boyunca bir sekansa eşleştirir. yakalama, başında köprüsü sonunda çevrimi ile aynı olduğu için, grup yolu kapanır.
- Eğer ki grup eklentisi yakalama ile ilişkili ise, prosedür U(1) etrafını sarar, manyetik yükü içeren bir küre şeklinde. Manyetik yük sarım sayısısı N ile doğru orantılıdır, küreden geçen akı 2πN/e eşittir. Bu, Dirac kuantizasyonu kuşuludur ve ayrıca uzak mesafe U(1) ölçü alanı konfigurasyonunun uyumlu olduğunu iddia eder.
- U(1) ölçü grubu kompakt Lie grubunu kırma durumundan geliyorsa, U(1) grubunun etrafını yeterik kadar saran yol büyük gruplar için çok önemlidir. U(1) olmayan kompakt Lie grubunda, saran uzayda bir Lie grubunu temsil eder çünkü aynı Lie cebirine sahiptir, fakat bu durum bütün kapalı döngülerin contractible olduğu zaman geçerlidir. Lie grupları homojendir, yani gurubtaki herhangi bir devir hareket ettirilebilir ki bu sayede bir kimlik kazandırılmaya başlanabilir., ardından çevreleyen gruba kaldırması P’da biter, ki bu da kimliğin yükselmesidir. Döngü üzerinde iki tur atmak sizi P2 durumuna getirir, üç tur atmak P3 durumuna getirir ve hepsi kimliğin yükseltilmesidir. Fakat sonlu sayıda, sınırlı, kimlik yükseltmesi olabilir çünkü yükselmeler birikemez. Bu sayıda bir küçük o kısaltılabilir yapmak için döngü geçmesi gerekir örneğin HUT grubu SO(3) ise, SU(2) kaplamak ve iki kez herhangi bir döngü dolaşma yeterlidir.
- Bu şu anlama gelir; BBT’deki sürekli bir ölçü alanı konfigurasyonu U(1) monopolünün kendini kısa bir mesafeiçin gevşetmesine olanak sağlar. Bunu mümkün olan en an enerji ile yapmak için sadece U(1)’den komşu olan bir noktada ayrılınabilinir ve bu noktada monopolün “çekirdeği” olarak isimlendirilir. Çekirdeğin dışında monopol sadece manyetik alan enerjisine sahiptir.
Bunun sonucu olarak, Dirac monopolü kompakt U(1) ölçü teorsiinde bir topolojik kusurdur. BBT olmadığı zamani kusur bir tekillliktir – çekirdek sadece bir noktaya büzüşür. Fakat uzay zamanda bir çeşit kısa-mesafe regülatörü olduğu zaman monopoller sonlu bir kütleye sahip olurlar. Monopoller latis U(1) içinde meydana gelirler ve içeride çekirdeğin boyutu latis boyutuna eşittir. Genel olarak, kısa-mesafe regulatörleri olduğu zaman meydana gelmeleri beklenir.
Sicim teorisi
Evrende, kuantum yerçekimi sağlar regülatörü sağlayan fenomendir. Kütleçekimi dahil olduğu zaman monopolün tekilliği bir kara delik olabilir ve ayrıca büyük kütle ve manyetik yük için kara delik kütlesi kara deliğin manyetik yüke eşit olur, yani manyetik kara deliğin kütlesi sonsuz olmaz. Eğer kara delik Hawking radyasyonu tamamen ışıma yaparsa, yüklü en hafif parçacık çok ağır olamaz.[7] En hafif monopol kendi yükünden daha az veya eşit kütleye sahip olmalıdır (doğal birimlerce)
Yani bu duruma karşılık gelen her holografik teoride-ki bir örneği de sicim teorisi daima sonlu kütleye sahip monopoller vardır. Sıradan elektromanyetizma için kütle üst sınırı pek kullanışlı değil çünkü yaklaşık olarak Planck kütlesi ile eşdeğerdir.
Matematiksel formülasyon
Matematikte (klsaik bir) ölçü alanı uzay zamanda temel G-demeti üzerinde bir bağlantı olarak tanımlanır. G ölçü grubudur ve her bir fiber demetine ayrı olarak davranır. G demeti üzerindeki Bir “bağlantı” fiberleri M civarı noktalarda nasıl birbirine yapıştıracağınızı söyler. Bir sürekli simetri grubu G ile başlar- ki bu grupta fiber F etkiler- ardından bütün sonsuz küçük yollar ile grup elemanını birleştirir. Herhangi bir yol boyunca grup çarpımı demet üzerinde, G elemanını fiber F ye etki eden bir yol ile ilişki bir şekilde sahip olarak, bir noktadan başka bir noktaya nasıl hareket edeceğinizi söyler.
Matematikte, demetin tanımı topoloji üstüne yoğunlaşmak üzere tasarlanmıştır, yani bağlantı kavramı sonra dan akla gelen düşünceler ile şekillenmiştir. Fizikte, bağlantı temel bir fiziksel objedir. Cebirsel topolojideki karakteristik sınıf teorisinde en temel gözlemlerden biri de nontrival prensip demetlerindeki birçok homotopik yapının herhangi bir baplantı üzerinde bir polinomun integrali ile açıklanma ihtimalidir. Unutmayınız;Trival demet asla bir nontrival prensip demeti vermez.
Eğer uzay zaman R4 G-demetinin bütün olası bağlantıları bağlanmıştır. Fakat uzayzaman dan hayat çizgisine sildiğimizi düşünelim. Bu durumun sonucu olan uzay zaman topolojk küre S2 homotopik eşitlik tir. G-demet formülasyonunda bir ölçü teorisi Dirac monopolünü kabul eder; her bir sabit yola deforme edilemez bir grup dolaşma yolları olacak şekilde bir G basit bağlantı olmadığı zaman. U(1), kuantize yüklere sahip bir U(1), basit bağlanmış değildir ve R- onun evrensel kavrama grubu- basit bağlanmış iken kuantize yüklere sahip değildir ve Dirac monopolünü kabul etmez. Matematiksel tanımı Dirac aşağıdaki şartıyla fizik tanımı, eşdeğerdir, gösterge alanları sadece yama bilge ve farklı yamaları göstergesi alan bir göstergesi dönüşümden sonra yapıştırılır tanımlandığı izin verilir. Toplam manyetik yük aslında bir topolojik invarianttır Tek kutuplular(monopoller)ın bu argümanı bir bakıma kement argümanının saf bir U(1) teorisi için yeniden belirtilmiş halidir. d + 1 ile d ≥ 2 boyutlarıyla birkaç yolla genelleşir.
Bir yöntem olarak her şeyi ekstra boyutlar ile açmak düşünülabilir ki bu sayede U(1) tek kutupluları d - 3 boyutunun düzlemi haline gelebilirler. Bir başka yöntem ise πd - 2(G) homotopi grubunda topolojik tekilliliği gözlemlemektir.
Büyük birleştirilmiş teoriler
Son yıllarda, yeni bir sınıf teoriler, ayrıca manyetik tek kutupların varlığını önerdi.
1970'li yıllarda elektrozaıf kuvvetler alanındaki kuantum alan teorisi ve ölçü teorisinin gelişmesi ve güçlü nükleer kuvvetlerin matematiği birçok teorisyeni bütün bu kuramları birleştiren bir büyük birleşik teori (BBT) bulmaya itti. Birkaç BBT önerildi ki bunların çoğuda gerçek manyetik tek kutuplu parçacığın varlığını ima etti. Daha kesin olmak gerkirse, BBT’ler dionlar olarak bilinen bir parçacıklar silsilesi önerdi; bu parçacıkların çoğunluğunun temel hali monopol idi. Kurama göre değişmekle beraber, manyetik monopollerin yükleri 1 veya 2 olarak BBTler tarafından öngörüldü.
Kuantum alan teorisindeki parçacıkların çoğu stabil değildir ve çok çeşitli tepkimeler -korunma kanununa uyan tepkimeler- başka parçacıklara bozunurlar. Stabil olan parçacıkların stabil olma sebebi ise ışıma yolu ile bozunmaya müsait parçacıklar olmamalrıdır ve ek olarak korunma kanunlarına uyarlar. Faraza, elektronun bir lepton sayısı=1 vardır ve elektrik yükü birdir ve bu değerleri koruduklarından ateşleyici(bozucu) parçacıklar değillerdir. Öte taraftan, müon,aslında elektronun ağır halidir, bir elektron ve iki enerji kuantasına bosunabillir, yani stabil değildir.
Bu BBT’lerdeki dionlar’da stabildir fakat tamamen farklı bir sebepten dolayı. Dionlar evrenin il koşulundaki dondurucu soğuğun kenar etkisi ile, veya simetri kırınımı, var olduğu beklenir.
Böyle bir senaryoda dionlar evrenin belirli yerlerindeki boşluk konfigurasyonundan dolayı oluşurlar, tabi Orijinal Dirac kuramına göre.Korunum koşulundan değil, bozunabilecekleri daha basit topolojik bir durum olmadığından stabil kalırlar.
Bu özel vakumlu yapılandırma var olduğu üzerinde uzunluk ölçeği sistemine 'korelasyon uzunluğu' denir. Korelasyon uzunluğu nedensellik fiziğinin Müsaade ettiğinden daha uzun olamaz, sonuç olarak manyetik tek kutuplu elde etmek için korelasyon uzunluğu en azından genişleyen evrenin metrik tensörnce belirlenen ufuk boyutları kadar uzun olmalıdır. .Bu mantığa göre, her bir hacime düşün ufukta en az bir manyetik tek kutuplu olmalıdır.
Büyük patlamaya süregelen olayların kozmolojik modelleri ufuk hacminin ne olduğuna dair tahmin yürütür ve bunlar, günümüz monopol yoğunluna dair tahminlere ön ayak olmuştur. Önceki modeller inamılmaz büyüklükte bir monopol yoğunluğu öngörmüştür; deneysel kanıtlara ters düşmesine rağmen.[8][9] Bu durum “tek kutuplu sorunu” olarak adlandırıldı.Bu sorunun genel kabul gören çözümü parçacık fiziğinin manyetik monopol tahmininde bir değişiklik durumu değildi ama daha çok günümzdeki yoğunluklarına ulaşmayı sağlayan kozmolojik modellerde idi. Özel olarak, kozmik genişleme daha güncel kuramları tahmin edilen tek kutuplu sayısını insanların şimdiye kadar neden rastgelmediklerini açıklarcasına şiddetle düşürdü.[10] Monopol problemine ilişkin bu yaklaşım, Parçacık fiziği'nde monopol kabulüyle kozmik genişleme'nin bir sonucu olarak düşünüldü[11]. İşbu nedenlerden dolayı monopoller 70'lerde ve 80’lerde BBT’lerin diğer “yaklaşılabilir” tahminleri (proton bozunumugibi) ile birlikte büyük bir ilgi gördü. BBT’ler tarafından öngörülen parçacıkların çoğu deneyler ile keşfedilmelin çok üzerindedir.Örneğin X ve Y bozonlar olarak bilinen geniş parçacık grubu elektrozayıf ve yeğin kuvvetler arasında ilişki kuracak bir bağ olara öngörüldü fakat bu parçacıklar inanılmaz ağırlıktadır ve bir parçacık hızlandırıcı tarafından yaratılması çok zordur.
Manyetik tek kutuplu arayışları
Manyetik tek kutupluları keşfedebilmek için çok sayıda deneme yapılmıştır. En basitlerinden biri “süperiletken kuantum girişim cihazı” veya SKGC kullanmak yani süperiletken tel ile bir döngü yoluyla çok küçük manyetik kaynakları incelemektir. Verilen bir yğunluktai laboratuvar masasına sığacak kadar küçük döngülerin yılda bir kez monopol durumu oluşturması öngörülür. Birçok boşuna umutlandıran olaylar kayıt altına alınmışsada, 14 Şubat 1982 tarihinde Blas Cabrera muhtemel monopolü çeren bir olay kaydetmiştir, (kimi zaman bu Sevgililer Günü monopolü olarak da anılır[12]) fakat, manyetik tek kutuplunun varlığına dair tekrarlanabilir bir kayıt bulunamamıştır.[13] P. Buford Price ve ekibi tarafından yürütülen 1975 yılındaki başka bir deneyle ise kozmik ışımada hareket eden bir manyetik tek kutuplunun keşfi duyurulmuştur.[14] Price iddiasını daha sonra dan geri çekmiştir ve olası bir alternatif çözüm Alvarez tarafından önerilmiştir.[15] Alvarez, çalışmasında manyetik monopol tarafından olduğu öne sürülen kozmik ışmanın yolunun aslında platinyum çekirdeğinin önce osmiyum daha sonra da tantalyuma nükleer bozunum suretiyle oluşmuş olabileceğini iddia etmiştir. Diğer deneyler de monopoller ile fotonlar arsındaki güçlü eşleşmeye güvenir, tıpkı herhangi bir elektrik yüklü parçacık için olan durum gibi. Parçacık hızlandırıcılar ile foton değişimi içeren deneylerde tek kutuplular mantıklı sayılarda üretilmelidir ve foton saçılımına etkilerinden dolayı tespit edilmelidir. Böyle bir parçacığın bu tarz bir olayda üretilme ihtimali, kütlesi ile doğru orantılıdır -daha ağır olan parçacıklar üreetilmeye daha az yatkındır- yani bu denylerin sonuçları incelenerek manyetik tek kutuplunun kütlesinin en büyük ve en küçük değerleri hesaplanabilir. Bu tarzda işleyen en güncel değerler 600 GeV/c2 kütlenin altında monopol olamaz – kütlenin üstlimiti ise evrenin varlığına göre değişir- ki bu da çok ağır olsalardı çökeceklerini gösterir. Büyük hadron çarpıştırıcısında inşa edilen MoEDAL deneyi makroskopik kara deliklerin manyetik alanı manyetik monopol olabilir, ki aslında bu da Einstein-Rosen köprüsüne bir giriş sayılır.[16]
Yoğun madde sistemlerinde tek kutuplu
Yaklaşık 2003 yılından beri kimi yoğun madde fiziği grupları çoğunlukla ilgisiz olan farklı olayları açıklamak için “manyetik monopol” terimini kullanıyorlar.[17][18] Gerçek bir manayetik tek kutuplu muhtemelen yeni bir temel parçacık olurdu ve manyetik alanı ihlal ederdi (B = 0). Bu tür bir monopol -ki bu tip bir monopol Paul Dirac tarafından 1931 yılında formüle edilen yük kuantizasyonu kuralını açıklamaya da yardımcı olurdu- henüz gözlemlenmemiştir.
Yoğun madde fiziği gruplarınca çalışılan tek kutuplu bu özelliklerin hiçbirini göstermezler. Yeni bir temel parçacığı teşkil etmezler, dah çok “günlük” parçacıkların (proton, nötron, elektron, foton) belirme teşkil eder. B-alanın kaynağı değildirler (B = 0]] inkar etmezler;) bunun yerine başka alanların kaynağıdırlar; örneğin H-alan,[19] ya da "B*-alan" (related to superfluid vorticity).[20]. Büyük birleştirilmiş teoriler ile veya parçacık fiziğinin başka yönleri ile doğrudan bağlantılı değildirler ve yük kuantizasyonunu açıklamaya yardımcı olmazlar – en azından benzeri durumlar hakkındaki çalışmalara mathematiksel analiz yardımcı olduğu sürece[21] yoğun madde fiziğinde kimi durumda spin buzunu [19][22] da içeren, manyetik monopolü andıran belirme fenomenine yol açan müşterek davranışa sahip birçok deney vardır.[23][24][25][26] Bütün bunlar vakumda var olan farazi temel monopoller ile karıştırılmaması gereksede, benzer özelliklere sahpler ve benzer teknikler kullanarak tanınabilirler.
Kimi araştırmacılar spin buzundaki manyetik monopol kuasi parçacıkları açıklamak için "manyetik (magnetricity)" terimini kullanırlar; "elektrik" sözcügüne benzetnek için.
Manyetik monopol quasiparçacıklarının hakkındaki çalışmaların bir örneğide Eylül 2009’da Science isimli dergide yayımlanan bir makaledir ve bu makale manyetik tek kutupluyu andıran quasiparçacığı tarif edilir.(makale Helmholtz-Zentrum Berlin für Materialien und Energie (HZB) ‘dan araştırmacılar Jonathan Morris ve Alan Tennant,Instituto de Física de Líquidos y Sistemas Biológicos (IFLYSIB, CONICET)’dan Santiago Grigera Dresden Teknoloji Üniversitesi’den diğer iş arkadaşları ile birlikte Oxford Universitesi ve St. Andrews Universitesi taradından yazılmıştır ).Spin buzu dysprosium titanate maddesinin tek bir kristali 0.6-2.0 kelvine kadar soğutulmuştur. nötron saçılımı gözlemi kullanılarak, tıpkı Dirac sicimlerinde olduğu gib manyetik momentlerin iç içe tüp benzeri demetler doğrultusunda hizalandığı gösterilmiştir. Her bir tüpün sonunda oluşan kusur, manyetik alanın tıpkı manyetik monopolün manyetik alanı gibi görünür. Sistemin simetrisini bozmak için manyetik alan uygulayarak, araştırmacılar sicimlerin yoğunluğunu ve yönelimini kontrol edebilmeyi sağladılar. Bu quasiparçacıklar etkili bir gaz sistemin ısı kapasitesi için bir katkı da tanımlanmıştır. [27][28] Bu araştırma, yoğun madde fiziği 2012 Europhysics Ödülü kazandı. Bir başka örnek ise 11 Şubat 2011 Nature Physics dergisinde yayımlanan, spin buzunda uzun ömrlü manyetik monopol quasiparçacık akımlarının üretilmesi ve ölçülmesi hakkında olan çalışma. dysprosium titanate kristaline 0.36 Kelvin sıcaklıkta atılan manyetik alan atımı uyguluyarak, araştırmacılar yedi dakika boyunca devam eden rahatlayan bir manyetik akım üretmeyi başarabildiler. Bu akımı hassas bir ampfilikatör iliştirilmiş selenoitte indüklenen elemktromotif kuvvetin kökleri ile bu hesaplamayı gerçekleştirebildiler ve aynı zamanda taşıyıcı ayrışma ve rekombinasyonun Onsager-Wien mekanizmasına uyan nokta şeklinde düşünülen yüklerin kimyasal kinetic modeli sayesinde niceliksle olarak açıklayabildiler. Yani, spin buzundaki monopol hareketin mikroskopik parametrelerini türettiler ve aynı zamanda serbest ve sınırlı manyetik yüklerin farklı rollerini tanımlamış bulundular.[29]
Süpersıvılarda süpersıvı çevrine bağlı bir manyetik alan B* vardır ve bu alanda matematiksel olarak manyetik B-alanına benzerdir. Bu benzerlik durumundan kaynaklanarak, B* alanı “sentetik manyetik alan” olarak adlandırılır. Haziran 2014’te B* alanı için monopol quasiparçacıklar[30] döner (spinor) Bose-Einstein yoğuşması[20] vasıtası ile yaratılır ve yine döner (spinor) Bose-Einstein yoğuşması vasıtası ile çalışılırlar. Bu durum, kauntum alan kuramı ile yönetilen (governed) bir sistem içinde gözlemlenen ilk quasi-manyetik tek kutup(monopol) örneğini teşkil eder.
Parçacık fiziğindeki daha ileri tanımlar
Fizikte “manyetik monopole” öbeği genellikle Yang–Mills potansiyeli A ile gösterilir ve Higgs alanı ϕ aşağıdaki Yang–Mills aksiyonu ile ifade edilir;
Matematikte yukarıdaki öbek (“manyetik monopole” öbeği) geleneksel olarak Bogomolny–Parasad–Sommerfeld limiti ile yukarıdaki denklemin durağan çözümü ile adlandırılır, ki aynı zamanda topolojik sınıf içinde fonksiyonun kesin minimumu (absolutes minimum of the function) şöyle olur;
yani şu anlama ifade eder; R3 vasıtası ile G-bundle]] üzerinde A ile bağlantı içerisindedir (ki aslında manifold -prensipte bir G objesi- ile de bağlantısı vardır) ve ayrıca Lie cebirininilintili adjoint demeti nin ϕ (kıvrımı FA ve kovaryant türevi DA ϕ Bogomolny equations denklemlerini sağlar;
ve sınır kuşullarını da sağlar;
80’lerden beri süregelen monopol terisindeki saf matematikteik gelişmeler sıklıkla fiziksel olarak motifli sorular üzerinden ilerledi. Denklemlerin ta kendisi ölçü dönüşümünde invaryanttır ve yönmelimi koruyan simetrilerdir. γ değeri büyük olduğunda ϕ ℝ3ten adjoint yörüngesin G/k’ya yarıçapı γ olan iki küre arasında bir eşleme tanımlar ve bu eşlemenin homotopi sınıfı manyetik yük olarak adlandırılır. Birçok iş yükün pzitif bir k tam sayısı olduğu G = SU(2), durumunda kullanılır. Ardından fonksyonelin mutlak minimum değeri 8πk olur ve katsayı m ϕ k/2 nin asimptotik açılım olur. İlk SU(2) çözümü 1975 E. B. Bogomolny, J. K. Parasad ve C. M. Sommerfield tarafından bulundu. Bu çözüm bir yükünün küresel simetrisidir ve aşağıdaki forma sahiptir;;
C.H.Taubes[31] 1980 yılında yapıştıran yapı ile gösterdi ki bütün büyük k değerleri için bir çözüm vardır-dır ve hemen ardından kapalı eksensel-simetrik çözümler bulundu. Genel durumlar ve k = 2 için ilk çözüm 1981’de R.S.Ward tarafından eliptik fonksionlarda sunuldu. Bogomolny denklemlerini çözmenin iki yolu vardır. İlk yol twistor metodudur. N.J. Hitchin,[32] in formülasyonunda keyfi bir çözüm TP1 karmaşık yüzeyi üzerinden bir holomorfoik vektör demetine karşılık gelir; projektif doğrunun teğet demetidir. Bu, R3’de yönelmil düz doğrulara doğal bir izomorfiktir. Sınırlayan koşul gösterir ki holomorfoik demet (k - 1)2 (the spectral curve) cins bir kompakt cebirsel eğri tarafından belirlenen bir açılımdır; belirli sınırlamaları karşılar. W.Nahm,[33] tarafından geliştirilen ikinci yöntem, Dirac operatörü için öz değer sorununun çözümünü içerir ve denklemleri sınır koşulları ile birlikte sıradan difaransiyel denklemlere çevirir; Nahm denklemleri;
burada Ti(s) ifadesi (0,2) fonksiyonunda değerli matrsitir. İki yapı da instanton için geçerli prosedürelere benzer prosedürler üzerine dayanır; N.S.Manton dan dolayı önemli olan gözlem R4’te Yang–Mills denklemleridir (c.f. ayrıca Yang–Mills alanı).
İki metodun SU(2 için eşitliği ve genel olarak uygulanabilirlikleri [34] ve [35] bahsedilmiştir. A ve ϕ için kapalı formüller iki yöntem içinde eldesi zordur; Nahm denklemlerinin simetrik durmlarda kimi tam değer veren çözümlere rağmen.[36] SU(n) ölçü grubu için Bogolomony–Parasad–Sommerfield limitinde maksimum gömülü küresel simetric manyetik monopol çözümleri [37][38] Gannoulis, Goddard ve Olive,[39] taradından temellendirildi ve Farwell and Minami [40] gösterdi ki Cartan matrix K level vektörü ile Lie cebirine karşılık gelen keyfi basit ölçü grubu için Bogolomony–Parasad–Sommerfield limitinde maksimum gömülü küresel simetrik manyetik monopol çözümleri Toda molecule[41][42] denklemlerinin çözümleridir;
Tekil olmayan çözümler orijinde manyetiik alan yok olması ile sonuçlanır. Lie cebirleri An, Bn ve Cn için Belirgen sonlu enerji çözümleri bu yöntem kullanılarak elde edilegelmiştir. Daha genel Lie group G durumu için -ϕ nin sonsuzdaki stabilizatörünün en büyük torus olduğu durumlarda, M.K.Murray[43] tarafından twistor bakış açısıyla -SU(2)-monopolünün tek spectral eğrisinin G Dynkin diagramınca endekslenen eğri koleksiyon ile değiştirildiği koşulda -ele alındı. Bu duruma karşılık gelen Nahm yapısı J.Hustubise ve Murray.[44] tarafından tasarlandı.
Ölçü eşitliğine kadar k yüklü SU(2) monopollerinin The moduli uzayı (c.f. also Moduli teorisi) Taubes[45] tarafından 4k - 1 boyutuna sahip kompakt olmayan pürüzsüz bir manifol olarak gösterildi. Ölçü dönüşümlerini (gauge transformations) sonsuzda bağlantıyı koruyacak şekilde kısıtlamak 4k-boyutlu manifold Mk verir, ki bu da gerçek modül uzayında çembersel demettir ve bir doğal, tamamlanmış hyper-Kähler metric [46] taşır.(c.f. also Kähler–Einstein manifoldu)
Ölçü twistor açısından bilinir ve Kähler potansiyeli spektral eğri Riemann theta fonksiyonları ile yazılabilir, ama sadece 2 durumda k = daha geleneksel ve kullanılabilir bir formda (2000) bilinmektedir. Bu Said–Hitchin manifold, Einstein Taub-metrik SOMUN ve ℝ4 olmayan triholomorphic SU(2) eylem ile sadece 4 boyutlu tam bir hiper-Kähler manifoldu vardır. Jeodezi onun monopole dynamics uygulamaya ilişkin Manton programı incelenmiştir. Daha fazla dinamik özellikler sayısal ve analitik teknikler tarafından izah edilmiştir. A cyclic k-fold conering of Mk splits isometrically is a product M̃k × S1 × ℝ3, where M̃k is the space of strongly centred monopoles. This space features in an application of S-duality in theoretical physics, and in[47] G.B.Segal and A.Selby studied its topology and the L2 harmonic forms defined on it, partially confirming the physical prediction. Üç hiperbolik alanı, manyetik Monopol bakış twistor noktasından M. F. Said tarafından (P1 × P1-çapraz anti tamamlayıcı Murray ve M. A. Şarkıcının ayrık Nahm denklemler açısından ve TP1 karmaşık yüzey değiştirme) incelenmiştir.
Ayrıca bakınız
- Horizon sorunu
- Düzlük sorunu
- Bogomolny denklemleri
- Dirac dize
- Dyon
- Felix Ehrenhaft
- Manyetizma için Gauss yasası
- Halbach dizisi
- İnstanton
- Meron
- Soliton
- 'T Hooft-Polyakov'un kutuplu
- Wu-Yang monopol
Notlar
- "Arşivlenmiş kopya". 1 Haziran 2016 tarihinde kaynağından arşivlendi. Erişim tarihi: 27 Mayıs 2016.
- Parker, C.B. (1994). McGraw-Hill Encyclopaedia of Physics (2nd bas.). McGraw-Hill. ISBN 0-07-051400-3.
- M. Mansfield, C. O’Sullivan (2011). Understanding Physics (4th bas.). John Wiley & Sons. ISBN 978-0-47-0746370.
- Wolfgang Rindler (Kasım 1989). "Relativity and electromagnetism: The force on a magnetic monopole". American Journal of Physics. 57 (11). American Journal of Physics. ss. 993-994. Bibcode:1989AmJPh..57..993R. doi:10.1119/1.15782.
- Jackson 1999, section 6.11, equation (6.153), page 275
- Nima Arkani-Hamed, Lubos Motl, Alberto Nicolis, Cumrun Vafa: The String Landscape, Black Holes and Gravity as the Weakest Force 19 Haziran 2014 tarihinde Wayback Machine sitesinde arşivlendi.(arXiv:hep-th/0601001, JHEP 0706:060,2007)
- Zel'dovich, Ya. B.; Khlopov, M. Yu. (1978). "On the concentration of relic monopoles in the universe". Phys. Lett. B79 (3). ss. 239-41. Bibcode:1978PhLB...79..239Z. doi:10.1016/0370-2693(78)90232-0.
- Preskill, John (1979). "Cosmological production of superheavy magnetic monopoles". Phys. Rev. Lett. 43 (19). s. 1365. Bibcode:1979PhRvL..43.1365P. doi:10.1103/PhysRevLett.43.1365.
- Preskill, John (1984). "Magnetic Monopoles". Annu. Rev. Nucl. Part. Sci. Cilt 34. s. 461. Bibcode:1984ARNPS..34..461P. doi:10.1146/annurev.ns.34.120184.002333.
- Rees, Martin. (1998). Before the Beginning (New York: Basic Books) p. 185 ISBN 0-201-15142-1
- "Arşivlenmiş kopya". 2 Ekim 2010 tarihinde kaynağından arşivlendi. Erişim tarihi: 27 Mayıs 2016.
- Alvarez, Luis W. "Analysis of a Reported Magnetic Monopole". ed. Kirk, W. T. (Ed.). Proceedings of the 1975 international symposium on lepton and photon interactions at high energies. International symposium on lepton and photon interactions at high energies, Aug 21, 1975. s. 967.
- "If the structures of the magnetic fields appear to be magnetic monopoles, that are macroscopic in size, then this is a wormhole." Taken from All About Space, issue No. 24, April 2014, item "Could wormholes really exist?"
- C. Castelnovo, R. Moessner and S. L. Sondhi (3 Ocak 2008). "Magnetic monopoles in spin ice". Nature. Cilt 451. ss. 42-45. arXiv:0710.5515 $2. Bibcode:2008Natur.451...42C. doi:10.1038/nature06433.
- S. T. Bramwell, S. R. Giblin, S. Calder, R. Aldus, D. Prabhakaran, T. Fennell (15 Ekim 2009). "Measurement of the charge and current of magnetic monopoles in spin ice". Nature. 461 (7266). ss. 956-959. arXiv:0907.0956 $2. Bibcode:2009Natur.461..956B. doi:10.1038/nature08500. PMID 19829376. 26 Nisan 2016 tarihinde kaynağından arşivlendi. Erişim tarihi: 27 Mayıs 2016.
- Making magnetic monopoles, and other exotica, in the lab 19 Nisan 2016 tarihinde Wayback Machine sitesinde arşivlendi., Symmetry Breaking, January 29, 2009. Retrieved January 31, 2009.
- Zhong, Fang; Nagosa, Naoto; Takahashi, Mei S.; Asamitsu, Atsushi; Mathieu, Roland; Ogasawara, Takeshi; Yamada, Hiroyuki; Kawasaki, Masashi; Tokura, Yoshinori; Terakura, Kiyoyuki (2003). "The Anomalous Hall Effect and Magnetic Monopoles in Momentum Space". Science. 302 (5642). ss. 92-95. arXiv:cond-mat/0310232 $2. Bibcode:2003Sci...302...92F. doi:10.1126/science.1089408.
- Inducing a Magnetic Monopole with Topological Surface States 2 Şubat 2009 tarihinde Wayback Machine sitesinde arşivlendi., American Association for the Advancement of Science (AAAS) Science Express magazine, Xiao-Liang Qi, Rundong Li, Jiadong Zang, Shou-Cheng Zhang, January 29, 2009. Retrieved January 31, 2009.
- " Artificial Magnetic Monopoles Discovered ". 6 Ekim 2013 tarihinde kaynağından arşivlendi. Erişim tarihi: 27 Mayıs 2016.
- "Magnetic Monopoles Detected in a Real Magnet for the First Time". Science Daily. 4 Eylül 2009. 10 Nisan 2016 tarihinde kaynağından arşivlendi. Erişim tarihi: 4 Eylül 2009.
- D.J.P. Morris, D.A. Tennant, S.A. Grigera, B. Klemke, C. Castelnovo, R. Moessner, C. Czter-nasty, M. Meissner, K.C. Rule, J.-U. Hoffmann, K. Kiefer, S. Gerischer, D. Slobinsky, and R.S. Perry (3 Eylül 2009) [2009-07-09]. "Dirac Strings and Magnetic Monopoles in Spin Ice Dy2Ti2O7". Science. 326 (5951). ss. 411-4. arXiv:1011.1174 $2. Bibcode:2009Sci...326..411M. doi:10.1126/science.1178868. PMID 19729617.
- S. R. Giblin, S. T. Bramwell, P. C. W. Holdsworth, D. Prabhakaran & I. Terry (13 Şubat 2011). "Creation and measurement of long-lived magnetic monopole currents in spin ice". 7 (3). Nature Physics. Bibcode:2011NatPh...7..252G. doi:10.1038/nphys1896. 4 Mart 2011 tarihinde kaynağından arşivlendi. Erişim tarihi: 28 Şubat 2011.
- Pietilä, Ville; Möttönen, Mikko (2009). "Creation of Dirac Monopoles in Spinor Bose–Einstein Condensates". Phys. Rev. Lett. Cilt 103. s. 030401. arXiv:0903.4732 $2. Bibcode:2009PhRvL.103c0401P. doi:10.1103/physrevlett.103.030401.
- A.Jaffe, C.H.Taubes (1980). Vortices and monopoles.
- N.J. Hitchin (1982). Monopoles and geodesics.
- W.Nahm (1982). The construction of all self-dual monopoles by the ADHM method.
- N.J. Hitchin (1983). On the construction of monopoles.
- N.J. Hitchin (1999). Integrable sustems in Riemannian geometry (K.Uhlenbeck bas.). C-L.Terng (ed.).
- N.J. Hitchin, N.S. Manton, M.K. Murray (1995). Symmetric Monopoles.
- F.A. Bais and H. Weldon, (1978). Exact Monopole Solutions in SU(N) Gauge Theory, Phys. Rev. Let. 41, 601.
- D. Wilkinson and F.A. Bais, (1979). Exact SU(N) monopole solutions with spherical symmetry, Phys. Rev D. 19, 2410
- N. Ganoulis, P. Goddard, D. Olive, (1982).Self dual Monopoles and Toda Molecules, Nucl. Phys. B205, 601
- Farwell, Ruth and Minami, Masatsugu, (1983). One-dimensional Toda Molecule. 2. The Solutions Applied To Bogomolny Monopoles With Spherical Symmetry, Prog. Theor. Phys. 70 710.
- M. Toda, (1975). Studies of a non-linear lattice, Phys. Rep., 8, 1.
- B. Kostant, (1979). The solution to a generalized Toda lattice and representation theory, Adv. in Math. 34, 195.
- M.K.Murray (1983). Monopoles and spectral curves for arbitrary Lie groups.
- Hurtubise, Jacques; Murray, Michael K. (1989). "On the construction of monopoles for the classical groups". Communications in Mathematical Physics. 122 (1). ss. 35-89. Bibcode:1989CMaPh.122...35H. doi:10.1007/bf01221407. MR 0994495. 5 Ağustos 2016 tarihinde kaynağından arşivlendi. Erişim tarihi: 27 Mayıs 2016.
- C.H.Taubes (1983). Stability in Yang–Mills theories.
- M.F. Atiyah; N.J. Hitchin (1988). The geometry and dynamics of magnetic monopoles. Princeton Univ.Press.
- G.B.Segal, A.Selby (1996). The cohomology of the space of magnetic monopoles.
Kaynakça
- Brau, Charles A. (2004). Modern Problems in Classical Electrodynamics. Oxford University Press. ISBN 0-19-514665-4.
- Hitchin, N.J.; Murray, M.K. (1988). Spectral curves and the ADHM method.
- Jackson, John David (1999). Classical Electrodynamics (3rd bas.). New York: Wiley. ISBN 0-471-30932-X.
- Milton, Kimball A. (Haziran 2006). "Theoretical and experimental status of magnetic monopoles". Reports on Progress in Physics. 69 (6). ss. 1637-1711. arXiv:hep-ex/0602040 $2. Bibcode:2006RPPh...69.1637M. doi:10.1088/0034-4885/69/6/R02.
- Shnir, Yakov M. (2005). Magnetic Monopoles. Springer-Verlag. ISBN 3-540-25277-0.
- Sutcliffe, P.M. (1997). BPS monopoles.
- Vonsovsky, Sergey V. (1975). Magnetism of Elemetary Particles. Mir Publishers.
- Misli, Ç. ve Yılmaz, O. "Aharonov-Bohm Olayı ve Monopol", ÇOMÜ FBE Dergisi, Cilt 2. 2016.
Dış bağlantılar
- Magnetic Monopole Searches (lecture notes)28 Ekim 2015 tarihinde Wayback Machine sitesinde arşivlendi.
- Particle Data Group summary of magnetic monopole search16 Mayıs 2017 tarihinde Wayback Machine sitesinde arşivlendi.
- 'Race for the Pole' Dr David Milstead 4 Mart 2016 tarihinde Wayback Machine sitesinde arşivlendi. Freeview 'Snapshot' video by the Vega Science Trust and the BBC/OU.
- Interview with Jonathan Morris 4 Mart 2016 tarihinde Wayback Machine sitesinde arşivlendi. about magnetic monopoles and magnetic monopole quasiparticles. Drillingsraum, April 16, 2010
- Misli, Ç. ve Yılmaz, O. "Aharonov-Bohm Olayı ve Monopol", ÇOMÜ FBE Dergisi, Cilt 2. 2016.
- Nature, 2009 31 Mayıs 2016 tarihinde Wayback Machine sitesinde arşivlendi.
- Sciencedaily, 200910 Nisan 2016 tarihinde Wayback Machine sitesinde arşivlendi.
- H. Kadowaki, N. Doi, Y. Aoki, Y.Tabata, T.J. Sato, J.W. Lynn, K. Matsuhira, Z. Hiroi (2009). "Observation of Magnetic Monopoles in Spin Ice". arXiv:0908.3568 $2.
- YouTube'da Video of lecture by Paul Dirac on magnetic monopoles, 1975
Şablon:SpringerEOM attribution
