Tork
Tork, kuvvet momenti ya da dönme momenti, bir kuvvetin nesnenin ekseninde, dayanak noktasında ya da çevresinde dönme eğilimidir. Kuvvet ister itme, isterse çekme olsun; tork bir nesnenin döndürülmesi olarak düşünülebilir. Matematiksel olarak, tork uzaklık vektörü ve devir üretilmesini sağlayan kuvvet vektörünün kaldıraç koluyla çapraz çarpımı olarak tanımlanır.
| Klâsik mekanik |
|---|
|
Dallar Statik · Dinamik / Kinetik · Kinematik · Uygulamalı mekanik · Gök mekaniği · Sürekli Ortam Mekanikleri · İstatistiksel mekanik |
|
Formüller
|
|
Temel kavramlar Uzay · Zaman · Hız · Sürat · Kütle · İvme · Yerçekimi · Kuvvet · İmpuls · Tork / Moment / Moment (fizik) · Momentum · Açısal momentum · Eylemsizlik · Eylemsizlik momenti · Gözlemci çerçevesi · Enerji · Kinetik enerji · Potansiyel enerji · İş · Sanal iş · D'Alembert ilkesi |
|
Konular Rijit cisim · Rijit cisim dinamiği · Euler denklemleri (rijit cisim dinamiği) · Hareket · Doğrusal hareket · Newton'un hareket yasaları · Newton'un evrensel kütle çekim yasası · Euler'in hareket yasaları · Hareket denklemleri · İvmeli referans çerçevesi · Eylemsiz referans çerçevesi · Yalancı kuvvet · Düzlemsel hareket mekaniği · Yerdeğiştirme (vektör) · Bağıl hız · Sürtünme kuvveti · Basit harmonik hareket · Uyumlu salınım · Titreşim · Sönümleme · Sönüm katsayısı Dönme hareketi Dairesel hareket · Düzgün dairesel hareket · Düzgün olmayan dairesel hareket · Dönen referans çerçevesi · Merkezcil kuvvet · Merkezkaç kuvveti · Merkezkaç kuvveti (Dönen referans çerçevesi) · Tepkisel merkezkaç kuvveti · Coriolis kuvveti · Sarkaç · Teğet sürat · Dönme sürati · Açısal ivme · Açısal hız · Açısal frekans · Açısal yerdeğiştirme |
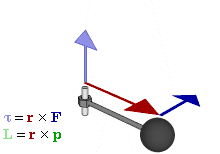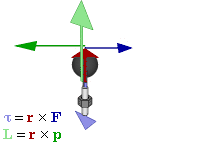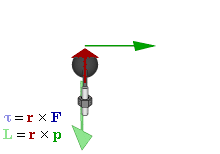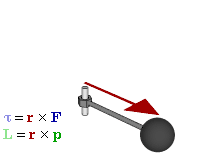
Genel olarak, tork cıvata ya da volan gibi nesnelerin üzerindeki dönme kuvvetinin hesaplanmasıdır. Örneğin, bir vida ya da cıvataya bağlı İngiliz anahtarını çekmek ya da itmek, vida ya da cıvatanın gevşemesi ya da sıkıştırılmasını sağlayan tork (dönme kuvveti) üretir. Tork sembolü genellikle Yunan Alfabesindeki tau, τ dır. Moment olarak adlandırıldığında ise, M olarak ifade edilir.
Torkun büyüklüğü şu üç özelliğe bağlıdır: uygulanan kuvvet, eksene bağlı kuvvet, uygulama noktasındaki kaldıraç kolunun uzunluğu ve kuvvet vektörü ile kaldıraç kolu arasındaki açının sin değeri.
Sembolik olarak;
T: Tork vektörü ve torkun büyüklüğü
R: Yer değiştirme vektörü (kuvvetin uygulandığı yerdeki torkun ölçüldüğü noktanın vektörü)
F: Kuvvet vektörü
θ: Teta kuvvet vektörü ile kaldıraç kolu vektörü arasındaki açı
Kaldıraç kolunun uzunluğu bilhassa önemlidir, bu uzunluğu seçmek kaldıraç, makara, dişli çarklar ve diğer mekanik avantaj içeren basit makinaların işleyişi altında yatmaktadır.
Uluslararası Birimler Sistemi’nde tork Newton metredir. (N.m). Daha detaylı bilgi, birimler kısmında verilecektir.
Tanım
Tork, matematiksel olarak bir nesnenin açısal momentumundaki değişimin oranı olarak tanımlanır. Torkun tanımına göre, bir nesnenin bir veya iki açısal hızı ya da eylemsizlik momenti değişmektedir. Ve moment terimi, uygulanan bir ya da birkaç kuvvetin nesneyi bir eksende dönmeye zorlaması eğilimi olarak kullanılmaktadır. Ancak genellikle nesnenin açısal hızı değişmemektedir (bu konsept fizikte tork olarak adlandırılır).
Örneğin, döndürücü kuvvet hızlanmaya sebep olan mile uygulandığında, geriye kalanı hızlandıran bir matkap gibi, elde edilen moment torktur. Tam aksine, bir kiriş üzerine uygulanan yan kuvvet moment (bükücü moment) üretir, ancak kirişin açısal momentumu değişmediği için, bu bükücü kuvvet tork olarak adlandırılamaz. Benzer şekilde, bir nesne üzerindeki kuvvet ikilisi açısal momentum üzerinde herhangi bir değişime sebep olmaz, bu şekilde bir moment de tork olarak adlandırılamaz.
Bu makale, nesnenin açısal momentumunun değişip değişmediğine bakmaksızın bütün momentleri tork diye adlandırarak Amerikan fizik terimlerini kullanmaktadır.
Tarihçe
Moment veya bağ diye adlandırılan tork kavramı, Arşimet’in kaldıraçlarla ilgili yaptığı çalışmaların üzerine kurulmuştur. Kuvvetin, kütlenin ve hızlanmanın dönüşsel analogları torktur, bunun yanı sıra eylemsizlik momenti ve açısal hızlanma da torktur.
Tanım ve Açısal Moment ile İlişkisi
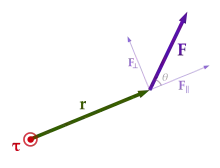
Bir kaldıracın sağ açısına uygulanan kuvvet kaldıracın kol uzunluğu ile çarpıldığında, tork elde edilir. 2 metrelik kaldıraç koluna 3 newton yük uygulandığında, veya 6 metrelik bir kaldıraç koluna 1 newtonluk kuvvet uygulandığından elde edilen tork aynıdır. Torkun yönü sağ el kuralı kullanılarak bulunabilir. Eğer sağ elin parmakları kaldıraç kolunun yönünden kuvvet yönüne doğru bükülürse, baş parmak torkun yönünü gösterir.
Daha genel manada, bir maddenin torku (bazı referans sistemlerinde r pozisyonuna sahip olan) çapraz çarpım olarak tanımlanabilir.
r parçacığının konum vektörü dayanağa yakın olduğunda, F bu parçacıkta hareket eden kuvvettir. Torkun τ büyüklüğü ise şöyledir:
r parçacığın dönüş ekseninden olan uzaklığı ise, F uygulanan kuvvetin büyüklüğüdür ve θ pozisyon ve kuvvet vektörü arasındaki açıdır. Alternatif bir yöntem ise;
F⊥ parçacığın pozisyonuna dik olarak uygulanan kuvvetin miktarıdır. Parçacığın pozisyon vektörüne paralel olarak uygulanan herhangi bir kuvvet tork üretmez.
Bu, tork vektörünün pozisyona ve kuvvet vektörüne dik olan çapraz çarpımın özelliklerini izler. Aynı zamanda torkun sebep olduğu, sonradan başlayan, yönü sağ el kuralı tarafından belirlenen dönüşün eksenini de gösterir.
Bir maddenin dönüş ekseni boyunca üzerindeki dengelenmemiş tork, maddenin açısal momentumunun değişim miktarını belirler:
L açısal momentum vektörü ve t de zamandır. Eğer birden fazla tork madde üzerinde çalışırsa, açısal momentumun değişim miktarını belirleyen şey net tork olur:
Sabit eksenin dönüşü ise:
I eylemsizliğin momenti ve ω açısal hızdır. Bunu takiben:
α maddenin açısal ivmesidir ve rad/s2 ile ölçülür. Bu denklemin şöyle bir sınırlaması vardır ki tork denklemi yalnızca dönüş ekseninin veya herhangi bir hareket türünün kütle merkezinin ani olduğu durumlarda yazılır- hareket isterse yalnızca geçiş, yalnızca dönüş ya da bu ikisinin karışımı olabilir. I, torkun yazıldığı eylemsizlik momentidir (ister ani eksen dönüşü ya da yalnızca kütle merkezi olsun). Eğer madde öteleme hareketinin dengesindeyse, tork denklemi hareket düzlemindeki bütün noktalarda aynıdır.
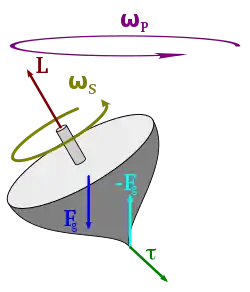
Tork yalnızca sabit eksen etrafındaki dönüşle sınırlı değildir. Açısal momentum vektörünün yönüne ya da büyüklüğüne göre değişebilir, hız vektörü ve kuvvet vektörünün ışınsal olmayan içeriklerin arasındaki açıya bağlıdır, bu durum dayanağın koordinat sisteminde gözlemlenebilir. Dönmekte olan nesnenin net torku, dönme hızında değişime yol açmaksızın devinime sebep olabilir.
Tanımların Denkliği Kanıtı
Tek bir parçacığın açısal momentumun tanımı şu şekildedir:
“x” çapraz çarpım vektörünü işaret ederken, p parçacığın doğrusal momenti, r ise orijinalin yer değiştirmiş vektörüdür. (orijinal hal, boşlukta herhangi bir yere sabitlenmiş konumdur.) Bu olayın zaman türevi:
Bu sonuç vektörleri bileşenlerine bölerek ve çarpma kuralı uygulanarak kolaylıkla kanıtlanabilir. Kuvvetin tanımını (kütle sabit olsun ya da olmasın) ve hız tanımını kullanarak
Hız (v) ile alakalı momentum çapraz çarpımının (p) sonucu sıfırdır çünkü hız ve momentum paraleldir, bu yüzden ikinci terim yok olur. Tanım olaraksa, tork τ = r × F dir. Dolayısıyla parçacık üzerindeki tork, zamanla ilişkili açısal momentumun ilk türevine eşittir. Eğer çift kuvvet uygulanırsa, Newton’un ikinci kuralını işaret eder Fnet = ma ve şunu izler:
Bu genel bir kanıttır.
Birimler
Tork, çeşitli kuvvet ebatlarının zaman mesafelerine sahiptir. Resmi Uluslararası Birimler Sistemi literatürü Newton metre birimi (N•m) ya da her radyanın joule biriminin kullanılmasını tavsiye eder. Newton metre birimi N•m ya da N m olarak gösterilir. Bu mN, milinewton arasında oluşacak karışıklığı önler.
Uluslararası Birimler Sistemi’nin enerji veya iş birimi jouledir. Bu, boyut olarak bir metre uzaklıkta hareket eden bir newtonluk kuvvete eşittir, ancak tork için kullanılmaz. Enerji ve tork tamamen farklı kavramlardır, bu yüzden farklı birim isimleri kullanmak (örneğin Newton metreleri tork için ayırmak ve enerjiler için sadece jul kullanmak) hatalardan ve yanlış anlaşılmalardan kaçınmayı sağlar. Birimlerin bu boyutsal eşitlikleri, basit bir tesadüf değildir: 1 N•m nin torku tam bir devir boyu uygulandığında 2π jul enerji gerekmektedir. Matematiksel olarak:
E enerji ise, τ torkun büyüklüğü ve θ hareket eden (radyanlarda) açıdır. Bu eşitlik alternatif birim ismi her radyan başı julü desteklemektedir.
İmperiyal birimlerde, “pound-kuvvet-fit” (lb•ft), “fit-pound-kuvvet”, “inç-pound-kuvvet”, “ons-kuvvet-inç” (oz•in) kullanılır ve diğer Uluslararası Birimler Sistemi’nde yer almayan tork birimleri “metre-kilogram-kuvvet” i içerir. Bütün bu birimlerde, “kuvvet” kelimesi çıkarılır, örneğin “pound-kuvvet-fit”, “pound-fit” olarak kısaltılır (bu durumda, “pound”un , pound kütlesi değil de pound kuvvetini ima ettiği söylenebilir). Bu, Uluslararası Birimler Sistemi ile kullanımı kaçınılması gereken geleneksel birimler tarafından yaratılan karışıklığa bir örnektir. Kullanımdan kaçınmak gerekir çünkü kuvvet (Newton) ve kütle (kilogram) arasında dikkate değer bir fark vardır.
Bazen tork için kullanılan birimlerin boyutsal olarak bir farkı olmadığı görülebilir. Örneğin, gram santimetre. Bu birimlerde, “gram” dünya üzerindeki 1 gram ağırlıktan, 0.00980665 N, verilen kuvvet olarak algılanabilir. Dünya yüzeyi yerçekimini hızlandıran bir standart olarak bilinir (9.80665 m/s2).
Özel Durumlar ve Diğer Gerçekler
Moment Kolu Formülü

Oldukça kullanışlı özel bir durumda, torkun fizik dışındaki diğer alanlardaki tanımı şu şekilde verilir:
Moment kolunun yapısı üstteki figürde, r ve F vektörleri ile gösterilmiştir. Bu tanımdaki problem torkun yalnızca büyüklüğünü verip, yönünü vermemesidir, ve bu yüzden bunu üç boyutlu durumlarda kullanmak zordur. Eğer kuvvet, yer değiştirme vektörü r ye dik ise, moment kolu merkeze olan uzaklığa eşit, ve torkta verilen kuvvet için en maksimum düzeyde olacaktır. Dik kuvvetten doğan tork büyüklüğünün denklemi:
Örneğin, eğer bir kişi 0.5 m uzunluğundaki (ya da herhangi uzunluktaki bir anahtarın dönme noktasından gelen 0.5 m lik 10 N kuvvet) anahtarın bağlantı ucunun sonuna 10 N lik bir kuvvet koyarsa, tork 5 N-m olacaktır, burada kişinin harekete alanındaki anahtara dik bir kuvvet uygulayarak anahtarı hareket ettirdiği varsayılır.
Durağan Denge
Bir nesnenin durağan dengede olması için, hem kuvvetlerin toplamının sıfır olması, hem de herhangi bir noktadaki torkların (momentlerin) toplamının sıfır olması gerekir. Yatay ve dikey kuvvetlerin olduğu iki boyutlu bir durumda, kuvvetlerin toplamı iki tür denklem gerektirir: ΣV = 0 ve torkun üçüncü denklemi de şudur: Στ = 0. Bu yüzden, iki boyutluların statikçe belirli denge problemlerini çözmek için, 3 denklem kullanılır.
Net Kuvvete Karşı Tork
Sistemin net kuvveti sıfır olduğunda, tork havada hangi noktada ölçülürse ölçülsün aynıdır. Örneğin, tekdüze mıknatıs alanındaki akım taşıma döngüsü üzerindeki tork, referans noktasına bakılmasızın aynıdır. Eğer net kuvvet sıfır değil ise, ve den ölçülen tork ise, den ölçülen tork şu şekildedir:
Makine torku
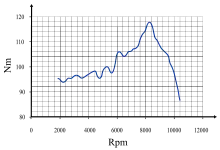
Tork bir motorun temel özelliklerinden biridir: bir motordan çıkan güç, eksenin dönüş hızıyla çarpılarak tork şeklinde ifade edilir. İçten yanmalı motorlar sadece limitli miktardaki dönüş hızı üzerinden tork üretirler (genelde küçük bir araç için 1,000-6,000 rpm dir). Bu değişken tork dinamometre ile ölçülür ve tork eğrisi olarak gösterilir.
Buhar makineleri ve elektrik motorları, maksimum sıfır rpm ye yakın tork üretme eğilimindedirler, dönüş hızı arttıkça tork azalmaktadır (artan sürtünme ve diğer kısıtlamalar yüzünden). Pistonlu buhar makineleri debriyajsız sıfır RPM den ağır yüklere başlayabilirler.
Tork, Güç ve Enerji Arasındaki İlişki
Eğer bir kuvvetin, bir yol boyu hareket etmesine izin verilirse, mekanik iş yapmış olur. Benzer şekilde, eğer tork dönüş mesafesi boyu hareket ederse, iş yapmış olur. Matematiksel olarak, kütle merkezi boyunca sabit eksen etrafındaki dönüş;
W iş, τ tork, θ1 ve θ2 maddenin ilk ve son açısal pozisyonunu gösterir (sırasıyla). Bu olay, iş-enerji teoremini destekler ki W aynı zamanda maddenin dönüşsel kinetik enerjisini Er gösterir:
I maddenin eylemsizlik momenti ve ω onun açısal hızıdır. Güç, her bir zaman birimindeki iştir;
P güç, τ tork, ω ise açısal hızdır ve içsel çarpımı ifade eder.
Matematiksel olarak, bu denklem belirli güç çıkışı için olan torku hesaplamak üzere tekrar düzenlenebilir. Şu dikkate alınmalıdır ki; tork tarafından verilen güç anlık açısal hıza bağlıdır – açısal hızın artması, azalması ya da tork uygulandığında sabit kalması önemsizdir (bu yalnızca anlık hıza bağlı kuvvet tarafından uygulanan gücün doğrusal durumuna eşittir, hızlanma sonucuna değil)
Pratikte, bu ilişki geniş elektrik gücü şebekelerine bağlı güç istasyonlarında gözlemlenebilir. Bu tip bir düzenlemede, jeneratörün açısal hızı şebekenin sıklığına bağlıdır, ve tesisin güç çıkışı jeneratörün dönme eksenine uygulanan torka bağlıdır.
Uygun birimler kullanılmak zorundadır, Uluslararası Birimler Sistemi’nin ölçü için birimlerinde güç watt, tork Newton metre ve açısal hız saniyedeki radyanlardır (rpm ya da saniyelik değişimler değildir).
Ayrıca, Newton metre biriminin ölçü olarak dengi bir enerji birimi olan juldür. Ancak, tork için, bu birim vektördür, enerji için ise, skalerdir.
Diğer Birimlere Dönüştürme
Dönüşme faktörü, farklı birimlerdeki güç, tork ya da açısal hız kullanırken gerekli olabilir. Örneğin, eğer dönüş hızı (devir sayısı) açısal hız (radyan sayısı) yerinde kullanılırsa, her devir 2π radyanla çarpılmalıdır. Bunu takip eden formüller, P güç, τ tork ve ω dönüşsel hızdır.
Diğer birimler:
Her 60 saniye için bölündüğünde ise;
Dönüşsel hız her dakikadaki devir sayısıdır (rpm)
Bazı insanlar (örneğin Amerikan otomotiv mühendisleri)güç için beygir gücünü (imperiyal mekanik), tork için fit-pound (lbf•ft) ve rpm için de dönüşsel hızı kullanırlar. Bu, formülün şu şekilde değişmesiyle sonuçlanır;
Bu aşağıdaki değişmezlik (dakikadaki fit poundları) beygir gücü tanımı ile değişir, örneğin, ölçü için beygir gücü kullanılırsa, bu yaklaşık olarak 32, 550 olur.
Diğer birimlerin kullanımı (örneğin saatteki güç için BTU) başka bir geleneksel değişim faktörü gerektirebilir.
Türeme
Dönen bir nesne için, dönüşün çevresi ile sarılan boyuna mesafe, açıyla sarılan radyanların ürününe eşittir. Bu demek olur ki: boyuna mesafe = radyan x açısal uzaklık. Ve tanım olarak, boyuna mesafe = boyuna hız x zaman = radyan x açısal hız x zaman. Torkun tanımı: Tork = radyan x kuvvet. Kuvveti hesaplayabilmek için şu şekilde değiştirebiliriz: Kuvvet = Tork ÷ Yarıçap. Bu iki değer güç tanımı için, birbiri yerine kullanılabilir:
Radyan r ve zaman t bu denklemden çıkarılmıştır. Ancak, açısal hız radyanlarda olmalıdır, doğrusal hız ve türemenin başlangıcındaki açısal hızın arasındaki doğrudan ilişki hesaba katılmalıdır. Eğer dönüş hızı her bir zaman birimindeki devir için hesaplanırsa, doğrusal hız ve uzaklık oransal olarak türemenin 2π yukarısındadır.
Eğer tork Newton metreyse ve dönüş hızı her saniyedeki devir sayısıysa, yukarıdaki denklem saniyedeki Newton metrelik ya da wattlık gücü verir. Beygirgücü denklemi ise her beygirgücü için 33,000 ft•lbf/d klik türeme faktörünün uygulanması ile elde edilir
çünkü
Moment Prensipleri
Varignon’un teoremi olarak da bilinen (aynı isimdeki geometrik teorem ile karıştırılmamalıdır.) moment prensipleri gösterir ki, tek bir noktaya uygulanan birkaç kuvvet sonucu oluşan torkların toplamı kuvvetlerin toplamına (sonucuna) eşittir. Matematiksel olarak, şu şekildedir:
Tork Çarpanı
Tork çarpanı, küçülme oranı 1 den büyük vites kutularıdır. Girdiye verilen tork, her bir küçülme oranı ile çarpılır ve çıktıya iletilir, dolayısıyla dönüş hızı azalmış, daha büyük bir tork elde edilir.
Kaynakça
Dış bağlantılar
- Power and Torque Explained A clear explanation of the relationship between Power and Torque, and how they relate to engine performance.
- "Horsepower and Torque"28 Mart 2007 tarihinde Wayback Machine sitesinde arşivlendi. An article showing how power, torque, and gearing affect a vehicle's performance.
- "Torque vs. Horsepower: Yet Another Argument"3 Mart 2009 tarihinde Wayback Machine sitesinde arşivlendi. An automotive perspective
- a discussion of torque and angular momentum in an online textbook14 Aralık 2010 tarihinde Wayback Machine sitesinde arşivlendi.
- Torque and Angular Momentum in Circular Motion 14 Mayıs 2017 tarihinde Wayback Machine sitesinde arşivlendi. on Project PHYSNET14 Mayıs 2017 tarihinde Wayback Machine sitesinde arşivlendi..
- An interactive simulation of torque22 Temmuz 2011 tarihinde Wayback Machine sitesinde arşivlendi.
- Torque Unit Converter19 Temmuz 2011 tarihinde Wayback Machine sitesinde arşivlendi.
