1 − 2 + 3 − 4 + · · ·

Matematikte 1 - 2 + 3 - 4 + ..., terimlerinin işaretleri sırasıyla değişen ardışık pozitif tam sayıların oluşturduğu sonsuz bir seridir. Serinin ilk m teriminin toplamı, Sigma toplama gösterimi kullanılarak şöyle ifade edilebilir:

\sum _{n=1}^{m}n(-1)^{n-1}

1 − 2 + 3 − 4 + … serisi kısmi toplamlarının ilk birkaç bin adedi

Bu sonsuz seri ıraksaktır çünkü kısmi toplamlarının dizisi (1, -1, 2, -2, ...) herhangi bir limit değere yakınsamaz. Ancak, 18. yüzyılın ortalarında Leonhard Euler, bir paradoks olduğunu kabul ettiği şu eşitliği yazmıştır:

1-2+3-4+\cdots ={\frac {1}{4}}

Buna yönelik titiz bir açıklama çok sonraları yapılabilmiştir. 1890'dan itibaren Ernesto Cesàro, Émile Borel ve diğerleri, Euler'in girişimlerine yeni yorumlar da getirecek şekilde, ıraksak serilere genellenmiş toplamlar atamak için iyi tanımlanmış yöntemler araştırdılar. Bu toplanabilirlik yöntemlerinin birçoğu, 1 - 2 + 3 - 4 + ... serisinin ¹⁄₄'e eşit olduğunu kolayca göstermektedir. Cesàro toplaması ise bu seriye bir değer atamayan az sayıdaki yöntemden biridir. Dolayısıyla bu seri, Abel toplaması gibi daha kuvvetli bir yöntemin kullanılması gereken serilere örnektir.

1 - 2 + 3 - 4 + ... serisi ile Grandi serisi (1 - 1 + 1 - 1 + …) yakından ilintilidir ve Euler tarafından, herhangi bir n için 1 - 2ⁿ + 3ⁿ - 4ⁿ + ... serisinin özel durumları olarak değerlendirilmişlerdir. Bu yaklaşım, Euler'in Basel problemi üzerindeki çalışmasını genişleten ve oradan da bugün Dirichlet eta fonksiyonu ile Riemann zeta fonksiyonu olarak bilinen fonksiyonel eşitliklere yönlendiren bir araştırma alanıdır.

Iraksaklık

Serinin terimleri (1, −2, 3, −4, …) hem + hem de − yönde 0'dan uzaklaştığı için, 1 − 2 + 3 − 4 + ... serisi terim testi bağlamında ıraksaktır. İleriki bahisler açısından, ıraksamayı temel bir yaklaşımla değerlendirmek de faydalı olur. Tanım olarak, sonsuz bir serinin yakınsama veya ıraksama niteliğini, o serinin kısmi toplamlar dizisinin yakınsaması veya ıraksaması belirler. 1 − 2 + 3 − 4 + ...'in kısmi toplamları ise şöyledir:[1]

1 = 1,

1 − 2 = −1,

1 − 2 + 3 = 2,

1 − 2 + 3 − 4 = −2,

1 − 2 + 3 − 4 + 5 = 3,

1 − 2 + 3 − 4 + 5 − 6 = −3,

...

Bu kısmi toplam dizisi serinin herhangi bir sayıya yakınsamadığını açıkça göstermektedir çünkü önerilecek herhangi bir x limiti için, belli bir noktadan sonra kısmi toplamların hepsinin [x-1, x+1] aralığının dışında olduğunu bulabiliriz. Dolayısıyla, 1 − 2 + 3 − 4 + ... ıraksaktır.

Bu kısmi toplam dizisinin her bir tam sayıyı bir kez içermesi de dikkate değerdir çünkü $\mathbb {Z}$ tam sayılar kümesinin sayılabilirliğini gösterir.[2]

Toplama için buluşsal yöntemler

Kararlılık ve doğrusallık

1, −2, 3, −4, 5, −6, … terimleri basit bir düzen izlediği için, kaydırma ve terim terim toplama yöntemini kullanarak, 1 − 2 + 3 − 4 + … serisi sayısal bir değer verecek şekilde düzenlenebilir. Herhangi bir s sayısı için s = 1 − 2 + 3 − 4 + … eşitliği yazılabiliyorsa, aşağıdaki düzenlemeler s = ¹⁄₄ eşitliğini göstermektedir:[3]

4s = (1-2+3-4+5-6+...)+(1-2+3-4+5-6+...)+(1-2+3-4+5-6+...)+(1-2+3-4+5-6+...)

= (1-2+3-4+5-6+...)+1+(-2+3-4+5-6+...)+1+(-2+3-4+5-6+...)+1-2+(3-4+5-6+...)

= (1-2+3-4+5-6+...)+1+(-2+3-4+5-6+...)+1+(-2+3-4+5-6+...)-1+(3-4+5-6+...)

= (1+1-1)+(1-2-2+3)+(-2+3+3-4)+(3-4-4+5)+(-4+5+5-6)+...

= (1)+(0)+(0)+(0)+(0)+...

= 1

ve

s = ¹⁄₄

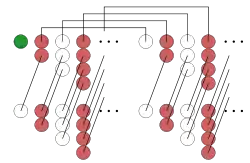
Yalnızca kaydırma ve terim terim toplama yöntemi kullanılarak 1 − 2 + 3 − 4 + … serisinin dört kopyası toplandığında, 1 elde edilir. Şeklin her iki yanında, 1 − 2 + 3 − 4 + …'in iki kopyasının 1 − 1 + 1 − 1 + ….'e eklenmesi gösterilmiştir.

Bu çıkarım, sağdaki şekilde grafik olarak anlatılmaktadır.

1 − 2 + 3 − 4 + …'in alışılmış anlamda bir toplamı olmasa da eğer bir toplam tanımlanacaksa, s = 1 − 2 + 3 − 4 + … = ¹⁄₄ eşitliği bunun en doğal yanıtı olarak desteklenebilir. Iraksak bir serinin "toplamı"nı gösteren genellenmiş bir tanım, toplama yöntemi ya da toplanabilirlik yöntemi olarak adlandırılır. Bu yöntem, tüm olası ıraksak serilerin bazı alt kümelerini toplar. Kimileri aşağıda anlatılmış olmak üzere, sıradan toplama ile paylaştıkları özelliklerine göre betimlenen pek çok değişik yöntem vardır. Yukarıda gösterilmiş düzenlemelerin bilfiil kanıtladığı ise şudur: doğrusal ve kararlı olan herhangi bir toplama yöntemi ile 1 − 2 + 3 − 4 + … serisi toplandığında, elde ettiği sonuç ¹⁄₄ olur.

Ayrıca bu yöntem, Grandi serisi toplamını da 1 − 1 + 1 − 1 + … = ¹⁄₂ olarak hesaplamalıdır:

2s = (1-2+3-4+5-6+...)+(1-2+3-4+5-6+...)

= 1+(-2+3-4+5-6+...)+1-2+(3-4+5-6+...)

= (1+1-2)+(-2+3)+(3-4)+(-4+5)+(5-6)+...

= (0)+(1)+(-1)+(1)+(-1)+...

= 1-1+1-1+...

ve

2s = 2 x ¹⁄₄ = ¹⁄₂ 'den

1-1+1-1+... = ¹⁄₂

Cauchy çarpımı

1891'de Ernesto Cesàro, ıraksak serilerin titiz yöntemlerle kalkulus bünyesine alınabileceklerine ilişkin görüşünü dile getirmiş ve bunu, "(1 − 1 + 1 − 1 + …)² = 1 − 2 + 3 − 4 + … eşitliğinin sağlandığı ve eşitliğin her iki tarafının ¹⁄₄'e eşit olduğu zaten biliniyor" diye ifade etmiştir.[4] Cesàro'ya göre bu eşitlik, bir önceki yıl yayınladığı ve muhtemelen de toplanabilir ıraksak seriler tarihinin ilk teoremi olarak tanımlanabilecek bir teoremin uygulamasıydı. Onun toplama yönteminin ayrıntıları aşağıda sunulmuştur; ana fikir ise 1 − 2 + 3 − 4 + … serisinin, 1 − 1 + 1 − 1 + … ile 1 − 1 + 1 − 1 + …'in Cauchy çarpımına eşit olduğudur.

İki sonsuz serinin Cauchy çarpımı, iki seri de ıraksak olsa bile tanımlıdır. Σa_n = Σb_n = Σ(−1)ⁿ koşulu sağlandığında, Cauchy çarpımının terimleri sonlu çapraz toplamlar ile ifade edilir.

{\begin{array}{rcl}c_{n}&=&\displaystyle \sum _{k=0}^{n}a_{k}b_{n-k}=\sum _{k=0}^{n}(-1)^{k}(-1)^{n-k}\\[1em]&=&\displaystyle \sum _{k=0}^{n}(-1)^{n}=(-1)^{n}(n+1)\end{array}}

Böylece, çarpım serisi

\sum _{n=0}^{\infty }(-1)^{n}(n+1)=1-2+3-4+\cdots

olarak yazılabilir.

Dolayısıyla, iki serinin Cauchy çarpımını temel alan ve 1 − 1 + 1 − 1 + … = ¹⁄₂ toplamını hesaplayabilen toplama yöntemi, 1 − 2 + 3 − 4 + … = ¹⁄₄'ü de bulacaktır. Önceki bölümün sonuçlarıyla birlikte bu, 1 − 1 + 1 − 1 + … ve 1 − 2 + 3 − 4 + …'in doğrusal, kararlı ve Cauchy çarpımını temel alan yöntemlerle toplanabilirlikleri arasında bir eşdeğerlik olduğunu gösterir.

1 − 1 + 1 − 1 + … serisi, Cesàro yönteminin en temel haliyle toplanabilirdir ve "(C, 1)-toplanabilir" olarak adlandırılır. 1 − 2 + 3 − 4 + … içinse bu teoremin daha güçlü bir biçiminin uygulanması gerektiğinden,[5] "(C, 2)-toplanabilir" olarak tanımlanır. Cesàro teoreminin tüm biçimleri doğrusal ve kararlı olduğundan, elde edilen toplamlar yukarıda hesaplandığı gibidir.

Özel yöntemler

Cesàro ve Hölder

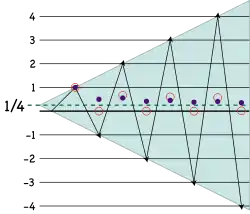
¹⁄₄'e eşit olan (H, 2) toplamına ilişkin veriler

Eğer varsa, 1 − 2 + 3 − 4 + … ifadesinin (C, 1) Cesàro toplamını bulmak için dizinin kısmi toplamlarının aritmetik ortalamalarını hesaplanmak gerekir. Kısmi toplamlar

1, −1, 2, −2, 3, −3, …

iken, bu kısmi toplamların aritmetik ortalamaları da şöyledir:

1, 0, ²⁄₃, 0, ³⁄₅, 0, ⁴⁄₇, …

Bu dizi yakınsak olmadığı için, 1 − 2 + 3 − 4 + … Cesàro yöntemiyle toplanamaz.

Cesàro toplamasının iyi bilinen iki genellemesi vardır. Bunların kavramsal bakımdan daha basit olanı, n doğal sayıları için kullanılan (H, n) yöntemler dizisidir. (H, 1), Cesàro toplamasını ifade etmektedir; daha üst düzey yöntemlerde de ortalama hesapları yinelenir. Yukarıda elde edilen ortalamalar dizisinde çift sıra numaralı olanlar ¹⁄₂'ye yakınsarken, tek sıra numaralı olanların tümü sıfırdır. Böylece, ortalamaların ortalaması, 0 ve ¹⁄₂'nin ortalaması olan ¹⁄₄'e yakınsar.[6] Sonuç olarak 1 − 2 + 3 − 4 + …, (H, 2) yöntemiyle ¹⁄₄ olarak toplanabilir.

"H", Otto Hölder'e karşılık gelmektedir. Hölder, matematikçilerin bugün Abel toplamı ve (H, n) toplamı arasındaki bağlantı olarak düşündükleri ilişkiyi 1882'de ilk kez kanıtlayan kişidir ve 1 − 2 + 3 − 4 + …'yi de ilk örnek olarak sunmuştur.[7] 1 − 2 + 3 − 4 + …'in (H, 2) toplamının ¹⁄₄'e eşit oluşu, bunun bir Abel toplamı olduğunu da garantilemektedir; bu ilişki aşağıda ıspatlanacaktır.

Cesàro toplamasının diğer genellemesi ise (C, n) yöntemler dizisidir. (C, n) ve (H, n) toplamalarının aynı sonucu verdiği kanıtlanmıştır ancak bu iki yöntem farklı tarihi köklere sahiptir. Cesàro, 1887'de (C, n) toplamasını tanımlamaya çok yaklaşmış ama sınırlı sayıda örnekler vermiştir. Yaptığı şey, bugün (C, n) olarak adlandırılabilecek ancak zamanında o şekilde doğrulanmamış bi yöntemle 1 − 2 + 3 − 4 + … toplamını ¹⁄₄ olarak hesaplamak olmuştur. (C, n) yöntemlerini 1890'da usule uygun şekilde tanımlayan Cesàro, (C, n)-toplanabilir bir seri ile (C, m)-toplanabilir bir serinin Cauchy çarpımının (C, m + n + 1)-toplanabilir olduğunu ortaya koyan teoremini bu tanıma dayandırmıştır.[8]

Abel toplamı

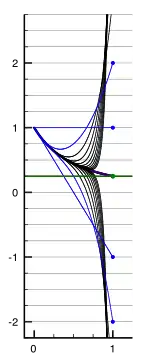
1−2x+3x²+…; 1/(1 + x)²'nin bazı parçaları ve 1 noktasındaki limitleri

Leonhard Euler, 1749 tarihli bir yazısında serinin ıraksadığını kabul etmekte ancak yine de toplamını hesaplamayı amaçlamaktadır:

« ... 1 − 2 + 3 − 4 + 5 - 6 + ... serisi toplamının ¹⁄₄ olduğu söylendiğinde, bunun bir paradoks olması gerekir. Çünkü serinin ilk 100 terimini toplayınca -50 elde ederiz, ilk 101 teriminin toplamı ise ¹⁄₄'ten oldukça farklı olan +51'i verir ve toplanan terim sayısı arttıkça da büyür. Daha önceki çalışmalarımda da gördüm ki, toplam sözcüğüne daha genişletilmiş bir anlam kazandırmamız gerek...[9] »

Euler, "toplam" sözcüğünün bir genellenmesini birçok kez önermiştir. Onun 1 − 2 + 3 − 4 + … serisine ilişkin görüşleri, bugün Abel toplaması olarak bilinen kavrama çok benzerdir:

« ... 1 − 2 + 3 − 4 + 5 - 6 + ... serisi toplamının ¹⁄₄ olduğuna artık şüphe yoktur çünkü seri, değerinin ¹⁄₄ olduğu tartışılmaz olan ¹⁄_(1+1)² formülünün açılımından kaynaklanmaktadır. Bu serinin, ¹⁄_(1+x)² ifadesinin açılımı olan 1 − 2x + 3x² − 4x³ + 5x⁴ − 6x⁵ + ... genel serisine x=1 için eşit olduğunun göz önünde bulundurulması, konuyu daha iyi açıklamaktadır.[10] »

En azından |x|<1 olan mutlak değerler için, Euler'in

1 − 2x + 3x² − 4x³ + ... = ¹⁄_(1+x)²

eşitliği konusunda haklı olduğu çeşitli yöntemlerle görülebilir. Eşitliğin sağ tarafının Taylor açılımı alınabilir ya da polinomlar için uzun bölme işlemi uygulanabilir. Sol taraftan başlandığında, yukarıda anlatılmış genel kestirme yöntemler izlenerek polinom (1+x) ile iki kez çarpılabilir ya da 1 − x + x² − …. geometrik serisinin karesi alınabilir. Ayrıca Euler, bu son serinin türevinin alınmasını da öneriyor gibidir.[11]

Modern görüşe göre, 1 − 2x + 3x² − 4x³ + … serisi x=1 için herhangi bir fonksiyon tanımlamaz; dolayısıyla da bu değer, elde edilen ifadedeki yerine doğrudan konamaz. Fonksiyon tüm |x|<1 değerleri için tanımlı olduğundan, x→1 (x, 1'e yaklaşırken) için limit alınabilir ve bu da Abel toplamının tanımını oluşturur:

\lim _{x\rightarrow 1^{-}}\sum _{n=1}^{\infty }n(-x)^{n-1}=\lim _{x\rightarrow 1^{-}}{\frac {1}{(1+x)^{2}}}={\frac {1}{4}}

Euler ve Borel

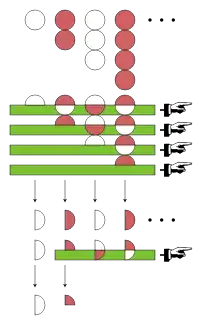
Serinin, Euler yöntemiyle ¹⁄₂ − ¹⁄₄'e toplanması

Euler, kendi ürettiği bir yöntem olan Euler dönüşümünü de bu seriye uygulamıştır. Euler dönüşümünü hesaplamaya, seriyi oluşturan pozitif tam sayıların dizisi olan 1, 2, 3, 4, …'den başlanır; dizinin ilk elemanı a₀ olarak adlandırılır.

Sonra, 1, 2, 3, 4, …'ün elemanları arasındaki ileri farkların dizisi hesaplanmalıdır. Sonuç 1, 1, 1, 1, …'e eşittir ve bu dizinin ilk elemanı ise Δa₀ diye adlandırılır. Euler dönüşümü, farkların farkları ve benzeri daha ileri tekrarlara da dayalıdır ama 1, 1, 1, 1, …'in tüm ileri farkları sıfıra eşittir. Dolayısıyla, 1 − 2 + 3 − 4 + …'nın Euler dönüşümü şöyle tanımlanır:

{\frac {1}{2}}a_{0}-{\frac {1}{4}}\Delta a_{0}+{\frac {1}{8}}\Delta ^{2}a_{0}-\cdots ={\frac {1}{2}}-{\frac {1}{4}}

.

Böylece, günümüz terminolojisiyle, 1 − 2 + 3 − 4 + … serisi Euler toplamının ¹⁄₄ olduğu ifade edilir.

Euler toplanabilirliği, farklı bir diğer toplanabilirliğe de işaret edebilmektedir. 1 − 2 + 3 − 4 + … serisinin

\sum _{k=0}^{\infty }a_{k}=\sum _{k=0}^{\infty }(-1)^{k}(k+1)

biçiminde ifade edilmesiyle, tümüyle yakınsak olan

a(x)=\sum _{k=0}^{\infty }{\frac {(-1)^{k}(k+1)x^{k}}{k!}}=e^{-x}(1-x)

serisi elde edilir. Böylece, 1 − 2 + 3 − 4 + … için Borel toplamı[12]

\int _{0}^{\infty }e^{-x}a(x)\,dx=\int _{0}^{\infty }e^{-2x}(1-x)\,dx={\frac {1}{2}}-{\frac {1}{4}}

olarak hesaplanır.

Ölçeklerin ayrılması

Saichev ve Woyczyński, yalnızca iki fiziksel ilke uygulayarak 1 − 2 + 3 − 4 + … = ¹⁄₄ eşitliğine ulaşırlar. Sonsuz küçüklükte gevşeme ve ölçeklerin ayrılması adlı bu ilkeler, onları seriyi ¹⁄₄'e toplayan geniş bir "φ-toplama yöntemleri" ailesini tanımlamaya yönlendirir:

φ(x), ilk ve ikinci türevi sürekli olan ve (0, ∞) aralığında integrali tanımlı bir fonksiyonsa ve φ(x) ile xφ(x)'in +∞'daki limitleri sıfıra eşitse,[13]

\lim _{\delta \rightarrow 0}\sum _{m=0}^{\infty }(-1)^{m}(m+1)\varphi (\delta m)={\frac {1}{4}}

sonucu elde edilir.

Bu sonuç, φ(x) yerine exp(-x) (¹⁄_e^x) konarak elde edilebilen Abel toplamının genellemesidir. Genel ifade, seri terimlerinin m üzerinde eşleştirilmesi ve ifadenin Riemann integraline dönüştürülmesiyle kanıtlanabilir. Sonraki adımda, 1 − 1 + 1 − 1 + … serisinin genel kanıtı için ortalama değer teoremi uygulanır. Ancak bu işlem, Taylor teoreminin daha güçlü olan Lagrange biçimine gerek duymaktadır.

Genellemeler

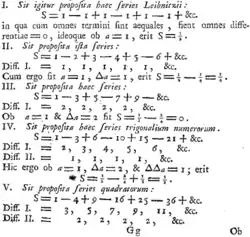
Tahminen 1755 tarihli E212 — Institutiones calculi differentialis cum eius usu in analysi finitorum ac doctrina serierum'den bir bölüm: Euler, benzer serilerin toplanışını gösteriyor.

1 − 1 + 1 − 1 + …'in üç katlı Cauchy çarpımı olan 1 − 3 + 6 − 10 + …, üçgensel sayıların almaşık serisidir. Bu serinin Abel ve Euler toplamı ¹⁄₈'dir.[14] 1 − 1 + 1 − 1 + …'in dört katlı Cauchy çarpımı 1 − 4 + 10 − 20 + … ise tetrahedral sayıların almaşık serisidir ve Abel toplamı ¹⁄₁₆'dır.

1 − 2 + 3 − 4 + …'in biraz daha farklı bir genellemesiyse, n'in farklı değerleri için 1 − 2ⁿ + 3ⁿ − 4ⁿ + … serisidir. Pozitif n tam sayıları için bu dizinin Abel toplamı aşağıdaki gibidir; formüldeki B_n, Bernoulli sayılarını ifade eder:[15][16]

1-2^{n}+3^{n}-\cdots ={\frac {2^{n+1}-1}{n+1}}B_{n+1}

n'in çift değerleri için,

1-2^{2k}+3^{2k}-\cdots =0

ifadesine sadeleşen bu toplam, Niels Henrik Abel'e 1826 yılında şöyle alay konusu olmuştur:

« "Iraksak diziler tümüyle şeytan işidir ve birinin bu dizilere kanıt araması utanç vericidir. Bunlardan istenileni elde etmek işten değildir ama bugüne dek karşılaşılan pek çok mutsuzluğun ve paradoksun sorumlusu da bu dizilerdir. n bir pozitif sayı olmak koşuluyla,

0 = 1 − 2ⁿ + 3ⁿ − 4ⁿ + vb.

ifadesinden daha dehşet verici bir şey düşünülebilir mi? İşte arkadaşlar, bu resmen gülünçtür.[17] »

Cesàro'nun öğretmeni Eugène Charles Catalan da ıraksak dizileri hor görmüştür. Öğretmeninin de etkisiyle Cesàro önceleri, 1 − 2ⁿ + 3ⁿ − 4ⁿ + … için üretilmiş "geleneksel" formülleri "saçma eşitlikler" olarak nitelemiş ve 1883'te de zamanın tipik görüşleri doğrultusunda, bu formüllerin yanlış olduğunu ancak bir şekilde işe yaradıklarını söylemiştir. Nihayet 1890'de, yazdığı Sur la multiplication des séries adlı yapıtında, tanımlardan başlayarak çağdaş bir yaklaşım sergilemiştir.[18]

1 − 2ⁿ + 3ⁿ − 4ⁿ + … serisi, n'in tam sayı olmayan değerleri için de incelenmiştir ki, bunlar Dirichlet eta fonksiyonunu oluştururlar. Euler'in 1 − 2 + 3 − 4 + … ile ilintili seriler üzerinde çalışmaya yönelmesinin bir nedeni, eta fonksiyonunun, doğrudan Riemann zeta fonksiyonu fonksiyonel eşitliğine yönlendiren bir fonksiyonel eşitlik olmasıdır. Euler, bu fonksiyonların pozitif çift tam sayılar kümesindeki değerlerini Basel problemini de içerecek şekilde bulmasıyla zaten ünlenmişti ve aynı başarıyı, Apéry sabitini de içerecek şekilde, pozitif tek tam sayılar kümesi için de yinelemeye çalışıyordu. Bu problem günümüzde hâlâ çözülememiştir. Eta fonksiyonu üzerinde Euler yöntemleriyle uğraşmak daha kolaydır çünkü bu fonksiyonun Dirichlet serisini, herhangi bir kompleks sayı için Abel yöntemiyle toplamak mümkündür. Zeta fonksiyonunun Dirichlet serisi ise ıraksamaya başladığı noktadan itibaren çok daha zor toplanır.[19] Örneğin, 1 − 2 + 3 − 4 + … serisinin zeta fonksiyonundaki karşılığı, işaretleri ardışık değişkenlik göstermeyen 1 + 2 + 3 + 4 + … serisidir. Bu serinin modern fizikte önemli uygulama alanları olsa da toplanması için çok daha güçlü yöntemler gereklidir.

Ayrıca bakınız

Kaynakça

Özel

Hardy (s. 8)
Beals (s. 23).
Hardy (s. 6).
Ferraro (s. 130).
Hardy (s. 3); Weidlich (s. 52-55).
Hardy (s. 9); Weidlich (s. 17-18)
Ferraro (s. 118); Tucciarone (s. 10).
Ferraro (s. 123–128).
Euler ve ark. (s. 2).
Euler ve ark. (s. 3, 25).
Lavine (s. 23) uzun bölmeyi önermekte ancak bu yöntemin uygulamasını göstermemektedir. Vretblad (s. 231) ise Cauchy çarpımını hesaplamaktadır. Euler'in önerisi belirsizdir; bkz. Euler ve ark. (s. 3, 26). John C. Baez, noktalı küme ve kuantum harmonik osilatörünün çarpımının yer aldığı bir kuramsal yöntem önermektedir. Baez, John C. Euler'in 1 + 2 + 3 + … = 1/12 Kanıtı (PDF). 30 Ekim 2012 tarihinde Wayback Machine sitesinde arşivlendi. math.ucr.edu (19 Aralık 2003). Erişim tarihi: 11 Mart 2007
Weidlich (s. 59)
Saichev ve Woyczyński (s. 260–264)
Kline (s. 313).
Hardy (s. 3).
Knopp, Konrad. (1990). Theory and Application of Infinite Series. New York: Dover Publications. s. 491. ISBN 0486661652. LCCN 89071388.
Grattan-Guinness (s. 80). Özgün Fransızca sürümünden başka bir çeviri için bkz.: Markushevich (s. 48)
Ferraro (s. 120–128).
Euler ve ark. (s. 20–25).

Genel

Beals, Richard (2004). Analysis: an introduction. Cambridge UP. ISBN 0-521-60047-2 23 Ekim 2015 tarihinde Wayback Machine sitesinde arşivlendi..
Davis, Harry F. (Mayıs 1989). Fourier Series and Orthogonal Functions. Dover. ISBN 0-486-65973-9.
Euler, Leonhard; Willis, Lucas; Osler, Thomas J. (2006). Translation with notes of Euler's paper: Remarks on a beautiful relation between direct as well as reciprocal power series10 Temmuz 2012 tarihinde WebCite sitesinde arşivlendi. The Euler Archive. (Orijinal yayın: Euler, Leonhard (1768). "Remarques sur un beau rapport entre les séries des puissances tant directes que réciproques". Memoires de l'academie des sciences de Berlin, 17:83–106)
Ferraro, Giovanni (Haziran 1999). "The First Modern Definition of the Sum of a Divergent Series: An Aspect of the Rise of 20th Century Mathematics". Archive for History of Exact Sciences, 54(2): 101–135. DOI 10.1007/s004070050036.
Grattan-Guinness, Ivor (1970). The development of the foundations of mathematical analysis from Euler to Riemann. MIT Press. ISBN 0-262-07034-0.
Hardy, G.H. (1949). Divergent Series, s. 8. Clarendon Press. Kongre Kütüphanesi kontrol numarası 91-75377.
Kline, Morris (Kasım 1983). "Euler and Infinite Series"21 Ağustos 2019 tarihinde Wayback Machine sitesinde arşivlendi.. Mathematics Magazine, 56(5):307-314.
Lavine, Shaughan (1994). Understanding the Infinite. Harvard UP. ISBN 0674920961.
Markushevich, A.I. (1967). Series: fundamental concepts with historical exposition. Hindustan Pub. Corp. Kongre Kütüphanesi kontrol numarası 68-17528.
Saichev, A.I. ve Woyczyński, W.A. (1996). Distributions in the physical and engineering sciences, Volume 1. Birkhaüser. ISBN 0-8176-3924-1
Tucciarone, John (Ocak 1973). "The development of the theory of summable divergent series from 1880 to 1925". Archive for History of Exact Sciences, 10(1-2): 1-40. DOI 10.1007/BF00343405.
Vretblad, Anders (2003). Fourier Analysis and Its Applications. Springer. ISBN 0387008365 23 Ekim 2015 tarihinde Wayback Machine sitesinde arşivlendi..
Weidlich, John E. (Haziran 1950). Summability methods for divergent series. Stanford Master of Science (master) tezi. Çevrim içi bilgisayar kütüphanesi merkezi: 38624384 19 Şubat 2009 tarihinde Wayback Machine sitesinde arşivlendi..

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Hardy (s. 8)

[2] Beals (s. 23).

[3] Hardy (s. 6).

[4] Ferraro (s. 130).

[5] Hardy (s. 3); Weidlich (s. 52-55).

[6] Hardy (s. 9); Weidlich (s. 17-18)

[7] Ferraro (s. 118); Tucciarone (s. 10).

[8] Ferraro (s. 123–128).

[9] Euler ve ark. (s. 2).

[10] Euler ve ark. (s. 3, 25).

[11] Lavine (s. 23) uzun bölmeyi önermekte ancak bu yöntemin uygulamasını göstermemektedir. Vretblad (s. 231) ise Cauchy çarpımını hesaplamaktadır. Euler'in önerisi belirsizdir; bkz. Euler ve ark. (s. 3, 26). John C. Baez, noktalı küme ve kuantum harmonik osilatörünün çarpımının yer aldığı bir kuramsal yöntem önermektedir. Baez, John C. Euler'in 1 + 2 + 3 + … = 1/12 Kanıtı (PDF). 30 Ekim 2012 tarihinde Wayback Machine sitesinde arşivlendi. math.ucr.edu (19 Aralık 2003). Erişim tarihi: 11 Mart 2007

[12] Weidlich (s. 59)

[13] Saichev ve Woyczyński (s. 260–264)

[14] Kline (s. 313).

[15] Hardy (s. 3).

[16] Knopp, Konrad. (1990). Theory and Application of Infinite Series. New York: Dover Publications. s. 491. ISBN 0486661652. LCCN 89071388.

[17] Grattan-Guinness (s. 80). Özgün Fransızca sürümünden başka bir çeviri için bkz.: Markushevich (s. 48)

[18] Ferraro (s. 120–128).

[19] Euler ve ark. (s. 20–25).