Kepler yörüngesi
Gök mekaniği olarak, Kepler yörüngesi (veya Keplersel yörünge) üç boyutlu uzayda iki boyutlu bir yörünge düzlemi oluşturan bir elips, parabol, hiperbol benzeri bir yörünge cismininin hareketini açıklar. (Kepler yörüngesi aynı zamanda düz bir çizgi de çizebilir). Kepler yörüngesi yalnızca nokta iki cismin nokta benzeri yerçekimsel çekimlerini dikkate alır, atmosfer sürüklemesi, güneş radyasyonu baskısı, dairesel olmayan gövde merkezi ve bunun gibi bir takım şeylerin diğer gövdelerle girdiği çekim ilişkileri nedeniyle ihmal eder. Böylece Kepler problemi olarak bilinen iki-cisim probleminin, özel durumlara bir çözüm olarak atfedilir. Klasik mekaniğin bir teorisi olarak, aynı zamanda genel görelilik etkilerini dikkate almaz. Kepler yörüngeleri çeşitli şekillerde altı yörünge unsurları içine parametrize edilebilir.
- Daha fazla benzer matematiksel gelişmeler için, iki cisim problemi, Yerçekimi iki cisim problemi, ve Kepler problemi’ni inceleyiniz..
Çoğu uygulamalarda, tüm sistemin kütle merkezi olarak kabul edilen büyük bir merkezi gövde ve kütle merkezi vardır. Ayrıştırma yapılınca, iki objenin benzer kütleleri, ikisinin ortak kütle merkezinin Kepler yörüngesi ya da barisentileri olarak açıklanabilir.
Giriş
Eski çağlardan itibaren 16. ve 17. yüzyıllara kadar gezegenlerin hareketlerinin Antik Yunan filozofları Aristo ve Batlamyus tarafından öğretildiği gibi mükemmel dairesel jeosentrik yolları takip ettiğine inanılırdı. Gezegenlerin hareketler değişimleri (epidaire) üst üste küçük dairesel yollar şeklinde açıklanmıştır.. Gezegenlerin ölçümleri giderek daha kesin olmaya başladığında, bu teoriye revizyonlar önerilmiştir. Hala gezegenlerin güneş merkezli mükemmel dairesel yörüngede gittiğine inanılmasına rağmen 1543 yılında Nicolaus Copernicus, güneş sisteminin bir güneş merkezli modelini yayınladı.
Johannes Kepler
1601 yılında Johannes Kepler Tycho Brahe tarafından yapılan gezegenlerin geniş, titiz gözlemlerini satın aldı. Kepler önümüzdeki beş yılını, çeşitli eğriler, Mars gezegeni gözlemlerini sığdırmaya çalışarak geçirecekti. 1609 yılında Kepler gezegensel hareketin üç yasasından ilk ikisini yayınladı. Birinci yasası:
“Her gezegenin yörüngesi odağı olan bir güneş çevresindeki elipstir.”
Daha genel anlatımla, Kerpler hareketini yapan bir objenin yolu elips olduğu kadar, parabol ve hiperparabol de olabilir. Bu bir grup şekil askonik kısımlar olarak bilinir. Matematiksel olarak, merkezi bir gövde ve bir yörüngedeki vücudun arasındaki mesafe olarak da ifade edilebilir:
- uzaklık
- yörüngesinin boyutunu tanımlayan yarı büyük eksen,
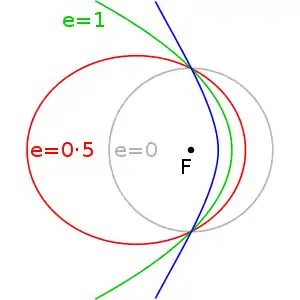
- yörüngesinin şeklini tanımlayan eksantrisite,
- anomali olduğunu, merkez gövde’ye (theperiapsis olarak adlandırılır ) en yakın yörüngedeki nesnenin geçerli konumunu ve yörüngede konum arasındaki açı olmak üzere:
Alternatif olarak, denkelm şu şekilde de ifade edilebilir.
eğrisi, yarı latus rektum olarak adlandırılır. Yarı-ana eksen sonsuz olduğu parabolik yörüngelerin ile uğraşırken denklem tarzı özellikle yararlıdır.
Bu yasalarını gözlemlerine dayandırmasına rağmen, Kepler’in bu hareketleri açıklamak için bir teori geliştirmesi mümkün olmamıştır.
Isaac Newton
1665 - 1666 yılları arasında, Isaac Newton hareket, yerçekimi ve diferansiyel hesap ile ilgili çeşitli kavramları geliştirmiştir. Ancak, bu kavramlar 1687 yılındaki Principia’ya kadar yayınlanmış değildi ki bu kitapta hareket yasalarının ve evrensel yerçekiminin altını çizmiştir. Hareket yasalarının üçünden ikincisi der ki:
Bir gövde ivmesi, paralel ve gövde üzerine etki eden net kuvvete orantılı olan net kuvvet yönünde olduğunu ve vücut kütle ile ters orantılıdır:
- vektör kuvveti
- kuvvetin uygulandığı gövdenin kütlesi
- hız vektörü, pozisyon vektörü ikinci kez diferansiyeli olmak üzere:
Açıkçası, denklemin bu formu yalnızca aşağıda yapılan basitleştirilmesi varsayımlara dayalı sabit kütleli bir nesne içingeçerlidir .
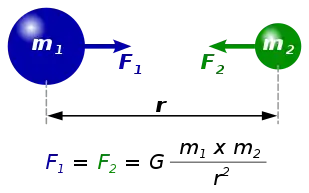
Newton'un yerçekimi yasası der ki:
Her nokta kütlesi, bir diğer nokta kütlesini çeker ve kuvvet noktası bu esnada iki noktadan da geçer.
Kuvvet noktası kitleler arasındaki mesafenin karesiyle ters orantılı iki kitlelerin ve ürüne orantılıdır.
- İki nokta kitleler arasında çekim kuvvetinin büyüklüğü
- yerçekimi sabiti
- ilk nokta kütlesi
- ikinci nokta kütlesi
- iki kütle arasındaki uzaklık olmak üzere:
Hareket ve evrensel çekim kanunu yasalarından, Newton gözlem ve teori arasındaki tutarlılığı gösteren, Kepler yasalarını elde etmeyi başardı. Albert Einstein 20. yüzyılın başlarında özel ve genel görelilik kavramları kadar Kepler ve Newton yasaları, modern gök mekaniğinin temelini oluşturmuştur. Çoğu uygulama için, Kepler hareket gezegenler ve uydular doğruluk nispeten yüksek dereceleri için hareketlerini yaklaştığı ve astronomi ve astrodynamics yaygın olarak kullanılmaktadır.
Basitleştirilmiş İki Cisim Problemi
(Ayrıca bakınız : Yörünge Analizi) Bir iki gövde sisteminde bir nesnenin hareketi için çözmek için, iki basitleştirici varsayım yapılabilir:
- 1.Gövdeler küresel simetriye sahiptir ve nokta kütleleri olarak değerlendirilebilir.
- 2.Gövdeler üzerinde ortak çekim kuvvetleri dışında, içten ya da dıştan etki eden bir kuvvet yoktur.
Büyük gök cisimlerinin şekilleri küreye yakındır. Simetri olarak, homojen bir küre doğru kitlesel bir noktaya çeken net çekim kuvveti kendi merkezine doğru yönlendirilmelidir. (Ayrıca Isaac Newton tarafından kanıtlanmış) kabuk teoremi, tüm kitle kürenin ortasında konsantre sanki bu kuvvetin büyüklüğü kürenin yoğunluğu en göksel için yaptığı gibi (derinlik ile değişse bile aynı olduğunu belirtmektedir organları). Bu hemen hem kütle merkezinde konsantre vardı sanki iki homojen küreler arasındaki cazibe olduğunu izler.
Asteroitler veya uzay gibi küçük nesneler, genellikle şekil kuvvetle bir küre sapma var. Ancak bu usulsüzlüklerin tarafından üretilen yerçekimi kuvvetleri merkezi vücut ağırlık karşılaştırıldığında genellikle küçük. Düzensiz şekil ve aynı zamanda mükemmel bir küre arasındaki fark mesafeleri ile azalır ve en yörünge mesafeler küçük yörüngedeki gövde çapına göre çok büyüktür. Böylece, bazı uygulamalar için, şekil düzensizlik doğruluğu üzerinde önemli etkisi olmadan ihmal edilebilir.
Gezegenler değişen oranlarda döndürmek ve böylece nedeniyle merkezcil kuvvet biraz basık şekli alabilir. Böyle bir basık şekli ile yer çekimi çekim homojen bir kürenin bundan biraz sapma olacaktır. Bu olay yapay uyduların Dünya, düşük yörüngelerde özellikle oldukça belirgindir. Büyük mesafelerde bu oblateness etkisi ihmal edilebilir hale gelir. Onlar nokta kitleler olarak kabul edilir ise Güneş Sistemindeki Gezegen hareketleri yeterli hassasiyetle hesaplanabilir.
İki nokta kütlesi bazı atalet referans çerçevesi deneyimi yer çekimi kuvvetlerine kitleler ve ve pozisyon vektör ve göreli ile nesneleri:
kütle 2'ye göre kütle 1 nispi konum vektörü:
yöndeki birim vektör ve bu vektörün uzunluğu
Kendi kitleleri bölünerek ve ikinci denklemden çıkarılarak, Birinci objenin hız hareketinin ikinci objeye göre denklemini buluruz.
-
(1)
yerçekim paremetresidir ve aşağıdakine eşittir.
Birçok uygulamada üçüncü ve daha basit bir çıkarım yapılabilir.
3. Merkezi gövde ile karşılaştırıldığında, yörüngedeki vücut kütlesi önemsizdir. Matematiksel olarak, m1 >> m²,
μ = G (m1 + m²) ≈ Gm1.
Bu varsayım basitleştirilmiş iki beden sorunu çözmek için gerekli değildir, ancak özellikle uydular ve güneşin etrafında dönen gezegenlerin Dünya yörüngesinde birlikte hesaplanmalarını kolaylaştırır. Hatta Jüpiter'in kütlesi 1047 faktörü ile güneşin daha az, μ değerinde 0.096% bir hata teşkil edecek olan kayda değer istisnalar Dünya-Ay sistemi (81,3 kütle oranı), Plüton-Charon sistemi (8.9 kütle oranı) ve ikili yıldız sistemleridir.
Bu varsayımlar altında, iki gövde durumu, diferansiyel denklemler ile tamamen matematiksel olarak çözülebilir ve gezegensel hareket Kepler yasalarını takibi ile sonuçlanan yörüngeye "Kepler yörüngesi" denir. Güneş etrafındaki tüm Kepler yörüngelerinin yüksek doğruluk payı vardır. Küçük sapmaların nedeni gezegenler arasında çok zayıf yerçekimi konumlarıdır, ve Merkür durumunda genel görecelilik kurallarıdır.
Dünya'nın çevresindeki yapay uyduların yörüngeleri, adil bir doğruluk payıyla, Güneş'in çekim gücü, Ay ve Dünya nedeniyle Kepler yörüngelerinde minik değişiklikler olabilir. Hareket denklemi dikkate alınmaktadır (örneğin Güneş’in radyasyon basıncı ve atmosferik sürüklenme gibi) yerçekimsel olmayan yerçekimi kuvvetleri ile sayısal entegrasyon gerektiren yüksek doğruluk payı olan uygulamalarda, Kepler yörünge kavramları büyük önem taşımaktadır ve yoğun olarak kullanılır.
Kepler Elementleri
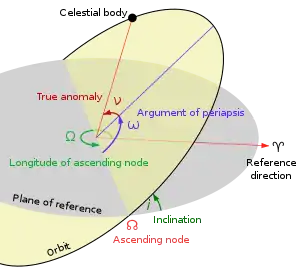
Kepler yörüngesinin altı parametre ile tanımlanabilirliğinden söz etmek gerekir. Üç boyutlu uzayda hareket eden bir nesnenin hareket bir konum vektörü ve bir hız vektörü ile karakterize edilir. Her vektörün üç bileşeni vardır, bu yüzden uzayda bir yörünge tanımlamak için gerekli değerlerin toplam sayısı altıdır. Bir yörünge (Kepler Elementleri olarak bilinen) ve pozisyon ve hızına bağlı olarak ölçülebilen altı elementten oluşur ki bunların üçü daha önce gösterilmiştir. Bu altı uygun elementten beş tanesi yörünge için değişmezdir. (iki sürekli değişen vektöre bir tezat niteliğinde olmak üzere). Kendi yörüngesinde içindeki bir nesnenin gelecekteki konumu tahmin edilebilir ve yeni konum ve hız kolayca yörünge elemanları ile elde edilebilir.
Bunlardan ikisi eksenin boyutunu ve şeklin belirler:
- Yarımajör eksen ()
- eksantriklik ()
Üç tanesi yörünge alanının oryantasyonunu belirler:
- eğim ()yörünge düzlemi ile referans düzlemi arasındaki açıyı tanımlar.
- Yükselen nodun uzunluğu () Referans yönü ve referans düzlemi üzerinde yörüngeye yukarı kesişme (yükselen nod) arasındaki açıyı tanımlar.
- Periapsis argüman() artan nod ve periapsis arasındaki açıyı belirler.
Ve son olarak:
- Gerçek anomali ()periapsis ölçülen yörünge boyunca yörüngedeki gövdesinin konumunu tanımlar.Çeşitli başka değerlerin yerine gerçek bir anomali kullanılabilir, bunlardan en sık kullanılanları mean anomoli olan ve periapsisden yana geçen süre olan ’dir.
, ve sadece yörünge düzlemi içinde nesnenin hareketini tartışırken referans çerçevesinde yörünge yönünü tanımlayan açısal ölçümlerdir ve kesin olarak gerekli değildir. Burada tamamlanmışlık adına belitilmişlerdir ancak aşağıdaki ispatlar için gerekli değillerdir.
Aşağıdaki diferansiyel denkleminin(1) Matematiksel Çözümü
Herhangi bir merkez kuvveti altında yani r bir kuvvet paraleli ve hareket için, belirli bağıl açısal momentumu sabit kalır:
Pozisyonun çapraz ürünü vektör ve onun hızı olduğu için sabit kaldığından, aynı düzelmde bulunmak zorundadırlar. (’ye ortogonal). Bu vektör, fonksiyonun, bir düzlem eğrisi olduğu anlamına gelir. Denklemin kökeni etrafında simetri vardır, çünkü kutupsal koordinatlarda çözmek kolaydır. Bununla birlikte, bu denklem dikkat etmek önemlidir 1 doğrusal ivmeye refere eder , açısalın karşıtı olarak yahut radyal ivmelenme. Bu nedenle, denklemi değiştiren kişinin dikkatli olması gerekir.Şimdi kartezyen koordinat sistemine ve kutupsal birim vektörlere düzlemi octoganelinde bakalım :
Şimdi vektör fonksiyonunu yeniden yazabiliriz ve diferansiyali şöyledir as:
(Vektör calculusunu inceleyiz). Bunları yerine yazarsak şunu buluruz:
(1)
Bu sıradan olmayan polar diferansiyel denklem verir:
-
(2)
Bu denklemi çözmek için, öncelikle her zaman diferansiyel lineerini ortadan kaldırmak gerekir.Şuna ulaşırız:
-
(3)
(3)’ün zaman diferansiyalinii aldığımız zaman, şuna ulaşırız:
-
(4)
(3) ve (4}) denklemleri ’ın diferansiyellerini elememize izin verir.. In order to eliminate the time derivatives of ’ın zaman diferansiyellerini ellimine etmek için uygun kısaltmaları bulmak bunun için de zincir kuralı kullanmamız gerekir.
-
(5)
-
(6)
-
(7)
Diferansiyel denklem (7) değişken değişimi ile analitik çözülebilir
-
(8)
Bu verilenleri kullanarak, in (2)’deki tüm zaman diferansiyelleri yoksayılabilir, ve bizi .
-
(10)
(10) ve (9)’da belirtilenleri ve için kullanarak
-
(11)
genel bir sonuca ulaşılır.
-
(12)
e ve ’un başlangıçtaki s ve ’n başlangıç değerlerinin integral sabitleri olursa, integralinin sabitini kullanmak yerine birim vektörleri kullanıma alınır ve seçilen yörünge alanındaki koordinat sistemini belirler, böylece sıfır değerini alır ve e is pozitiftir.Bu şu anlama gelir: ’in maksimum olduğu yerde sıfırdır ve böylece minimumdur. p parametresini olarak tanımlarsak şu ortaya çıkar
Alternatif Türevleri
Bu denklemi polar diferansiyel denklemini kullanmadan çözmenin bir diğer yolu şöyledir:
‘yu bir birim vektör olarak tanımlayın, örneğin, and gibi . Burdan yola çıkarak
Şimdi şunu değerlendiriniz
(Üçlü vektör ürünü). Şunu dikkate alınız
Bu verileri bir önceki denkleme yerleştirdiğimizde
İki tarafın da integralini alırsak
Burada c sabit vektördür. Bunu r' ile birleştirmek ortaya ilginç bir sonuç çıkarır
Burada ve arasındaki açıdır. r’ye göre çözersek
Dikkat ediniz ki vektör fonksiyonunun polar kordinatlarıdır. Verilenleri yerine koyarsak ve , şu denkleme ulaşırız
-
(13)
Bu fokal noktada merkezi olan bir konik bölmenin polar kordinatlarının denklemidir. Argümanına gerçek anomali denir.
Yörünge Denkleminin Özellikleri
ise bu çapı p olan bir dairedir.
ise bu aşağıdakine sahip bir elipstir.
-
(14)
-
(15)
ise fokal uzunluğu olan bir dairedir. ise bir aşağıdakine sahip bir hiperboldür.
-
(16)
-
(17)
Sonraki görsel, bir elipsi (kırmızı), bir paraboolü (yeşil) ve bir hiperbolü (mavi) gösterir.

Yatay çizgi üzerinde nokta odak noktasından sağa doğru çıkıyorsa nokta odak noktasına olan minimum uzaklık değerini alır (pericentre) .Elips için de odak uzaklığı maksimum değerini aldığı bir apocentre vardır. Hiperbol için ’nın aralığı:
Bir parabol için aralık;
Diferansiyelin zinci kuralını kullanarak (5),(2) denklemi ve p’nin tanımı olmak üzere radyal hız elemanı şudur.
-
(18)
ve teğetsel bileşen olan (hız bileşeni )’ye dik )
-
(19)
Polar argümanı ve zaman t arasındaki bağlantı elips ve hiperbolik yörüngeler için küçük değişiklikler gösterebilir.
Elips şeklindeki bir yörünge için, dış merkezli anomali olan E’ye geçeriz ve burdan
-
(20)
-
(21)
ve sonuç olarak.
-
(22)
-
(23)
açısal momentum H olmak üzere
-
(24)
Zamana göre entegrasyon olan t ile şu sonuca ulaşılır.
-
(25)
zaman varsayımını yaparak integral sabiti 0 olur. p nin tanımı gereği
-
(26)
şu şekilde yazılabiir
-
(27)
Hiperbolik bir yörünge için parametre yaratmak için hiperbolik fonksiyon kullanılır.
-
(28)
-
(29)
bu durumda şuna ulaşılır
-
(30)
-
(31)
açısal momentum H olmak üzere
-
(32)
Zamana göre entegrasyon olan t ile şu sonuca ulaşılır.
-
(33)
örneğin
-
(34)
t’nin hangi zamanda belirli bir gerçek anomaliye () ne ulaştığını bulmak için, buna uyan parametre olan E’nin (27) ile zamana olan bağını hesaplaması, elips için (34) ile bağını ve hiperbolik yörünge için.
Bazı Ek Formüller
Ayrıca bakınız: Merkez denklemi - analitik açılımlar
(20)ve (21)’den edilinen elips yörünge için
-
(35)
ve buna göre
-
(36)
(36)’dan devam ettiğimizde şu sonuç çıkar
Dış merkezli anomalinin geometrik yapısını belirlemek için, açıkça vektörler ve ‘nin x aksisiyle aynı yanda olmaları gerekir. Buradan yola çıkarak ve aynı çeyrek daireye sahiptir. Burdan yola çıkarak
-
(37)
ve
-
(38)
-
(39)
vektörünün polar argümanlarınınve n "" örneğinde olduğu gibi seçilmiş olması gerekir.
nın sayısal hesaplaması için, standart ATAN2(y,x) fonksiyonunun, ( ya ikili DATAN2(y,x)), FORTRAN gibi programlama dillerinde kullanılması mümkündür.
Dikkate alınız ki bu aralıklar arasında alan vardır.
Hiperbolik bir yörünge için (28) ve (29)dan yola çıkarak
-
(40)
and therefore that
-
(41)
ve sonuç olarak
ve aşağıdaki ifadeyi sağlayan aynı işarete sahiptir.
-
(42)
Bu ilişki gerçek anomali ve E parametresi arasında geçiş yapmak için uygundur. (burada E (34)’e zaman yönünden bağlıdır.) Aralık arasındaki alana dikkat ediniz.
ve aşağıdaki bağla açıklanabilir.
(27)’ye bakarak, P’nin elips bir yörünge için yörünge periyodu
-
(43)
Kuvvet alanına potansiyel enerjinin ilgisi (1)
(13), (14), (18) ve (19)’ kadar kinetik ve potansiyel enerjinin özeti
Elips yörünge için
-
(44)
(13), (16), (18) ve (19)’den sonra kinetik ve potansiyel enerjinin hiperbol yörünge için
Eylemsizlik koordinat sistemiyle ilişkisi
-
(44)
and from (13), (16), olan bir yörünge düzleminde pericentre’ye doğru (18) ve (19)’dan yapılan hız elementleri çıkarımı
-
(45)
Belirli bir başlangıç durumuna karşılık Kepler yörüngesinin belirlenmesi
Bu diferansiyel denklemi (1) için "başlangıç değeri problemi" dir, ki 6 boyutlu bir durum vektründe ilk denklemdir ve şöyle yazılır
-
(46)
-
(47)
Başlangıç değeri vektörünün herhangi bir değeri için, bu başlangıç değeri probleminin çözümüne uygun Kepler Yörüngesi aşağıdaki algoritmayla bulunur
Ortogonal birim vektörleri tanımalamak gerekirse
-
(50)
-
(51)
ve and
(13), (14), (18) ve (19)’dan sonra sırasını takip eder.
|
(52) |
and ‘yı tanımlarken
-
(53)
-
(54)
aşağıdakinin olduğu yerde
|
(55) |
aynı r, and değerlerine sahip olan gerçek anomaliye sahip bir Kepler yörüngesi bulunur ve bu (50) ve (51)’de gösterilmiştir.
Eğer bu Kepler yörüngesi aynı vektörlerine sahipse ve gerçek anomalisi (50) ve (51)de tanımladığı gibi ise, Kepler yörüngesinin vektörleri istenen değer olan ’yi gerçek anomalisi olmak üzere alır.
Standart atalet sabit koordinat sistemi yörüngesel düzlemde ( pericentre'nin homojen küresindin merkezinden gelecek şekilde) konik alanın oryantasyonunu belirliyorsa (elips, parabol, hiperbol), bu ilişkiyle hesaplanabilir.
|
(56) |
|
(57) |
(53) ve (54)’ün olduğu durumda bağlantılı olduğuna dikkat ediniz ve
örneğin
|
(58) |
Diaresel bir yörüngeye uyan başlangıç durumunu gösterir.
Öskülatör Kepler Yörüngesi
Ana makale: Öskülatör Yörünge gibi herhangi bir durum vektörü için, bu durumdaki Kepler yörüngesi aşağıda tanılmlanan algoritma ile hesaplanabilir. İlk parametreler ile belirlenir ve yörüngesel düzelemde ortogonal birim vektörleri de (56) ve (57) arasındaki ilişkiyi kullanarak bulunur.
Şimdi, eğer hareket denklemi aşağıdaki gibi ise
|
(59) |
aşağıdakinin
bir fonksyion olup
aşağıdaki parametlere sahip olmaması gerekir.
tarafından tanımlanmış, zaman içinde değişecek olan durumlar, Keppler Yörüngesinin tersine yalnızca ’da değişecektir.
T zamanında bu şekilde "hareket denkleminin" çözümü olarak aynı "durum vektör" olan (Şablon:Denklem notu59) 'de hesaplanan Kepler yörüngesi bu durumda "öskülatör" olduğu söylenebilir. Bu konsept, şu durumda yararlıdır.
olmak üzere
küçük bir “bozucu güç”tür çünkü, bir örnekle açıklamak gerekirse diğer gök cisimlerindensönük bir yer çekimi bu durumda örnek gösterilebilir. Öskülasyon halindeki Kepler yörüngesinin parametreleri, ancak o zaman yavaşça değişecek ve öskülasyon halindeki Kepler yörüngesi iyi bir tahminle öskülasyonun öncesinde ve sonrasnda gerçek yörüngeye hatrı sayılır bir zaman diliminde girecektir. Bu konsept aynı zamanda bir roket uçuşu için de faydalı olabilir çünkü itme kapatıldığı zaman hangi Keppler yörüngesinde devam edebileceği belirlenmiş olur. “Daire olmaya yakın” bir yörünge konsepti için, dışmerkezli vektörü şeklinde tanımlamak yararlıdır. (53), (54) ve (56)’dan yola çıkarak:
-
(60)
Örneğin durum vektörlerinin diferansiyel fonskyonlarıdır , ayrıca bu durum dairesel bir yörüngeye karşılık geliyor ise de geçerlidir.
Ayrıca bakınız
- Kepler's laws of planetary motion
- Elliptic orbit
- Hyperbolic trajectory
- Parabolic trajectory
- Radial trajectory
- Orbit modeling