Diskriminant

Tek bilinmeyenli ikinci derecede bir polinom denklem ele alalım ve denklemde a, b ve c üç gerçel sayılı katsayı olsun ve a değeri 0 dan değişik olsun

${\displaystyle ax^{2}+bx+c=0}$

denklemi ve a ≠ 0 olsun.

Bu tek bilinmeyenli ikinci derecede polinom denklemin diskriminantı şöyle tanımlanan Δ (delta) sayısı ile ifade edilir:

${\displaystyle \Delta =b^{2}-4ac\;}$

Diskriminant'ın bilinmesi bu tek bilinmeyenli ikinci derece polinomun çözülmesini sağlar:

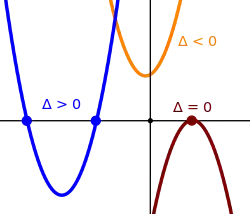
a) Δ > 0 yani Δ pozitif ise, denklemin farklı iki gerçel kökü vardır. x₁ ve x₂ olarak ifade edilen bu iki kök şu formül kullanılarak bulunur:

${\displaystyle x_{1}={\frac {-b+{\sqrt {\Delta }}}{2a}}\quad {\text{ ve}}\quad x_{2}={\frac {-b-{\sqrt {\Delta }}}{2a}}}$

b) Δ = 0 yani Δ sıfıra eşit ise, denklemin, değerleri birbirleriyle çakışan, yani birbirine eşit, iki gerçel kökü vardır:

${\displaystyle ax^{2}+bx+c=a(x+{\frac {b}{2a}})^{2}\quad {\text{et}}\quad x_{1}=x_{2}=-{\frac {b}{2a}}\;}$

c) Δ < 0 yani Δ negatif ise, denklemin gerçel kökü yoktur yani denklemin çözümü bulunamaz.

Eğer a, b ve c kompleks (karmaşık) sayılar ise veya denklemin çözümü için kompleks sayı kullanılması kabul edilmişse durum biraz daha değişiktir. D'Alembert-Gauss teoremine göre denklemin en aşağı bir tane çözümünün bulunması gerekir. Kompleks sayılıların ise her zaman iki tane kare kökü bulunur; yani öyle bir δ değeri vardır ki bunun karesi ( δ²) Δ'ya eşittir. Buna göre

a) Eğer diskriminant sıfır dan değişik bir değerde ise, denklemin iki çözüm değeri, yani x₁ ve x₂, şu formülle bulunur:

${\displaystyle x_{1}={\frac {-b+\delta }{2a}}\quad {\text{ ve }}\quad x_{2}={\frac {-b-\delta }{2a}}}$

b) Eğer diskriminant değeri sıfır ise denklemin çözümü olarak birbiriyle çakışmış eşit şu iki tane kök ${\displaystyle x_{1}}$ bulunur:

${\displaystyle x_{1}={\frac {-b}{2a}}}$

Bazen ikinci derecedeki polinom denklem şu şekilde yazılmaktadır:

${\displaystyle ax^{2}+2b'x+c=0\;}$

Bu şekilde değişik bir diskriminant bilinir ve bu kısaltılmış diskriminant (Δ') şöyle tanımlanır:

${\displaystyle \Delta '=b'^{2}-ac\;}$

Eğer bu denklemin kökleri varsa, şöyle bulunurlar:

${\displaystyle x_{1}={\frac {-b'+\delta '}{a}}\quad {\text{et}}\quad x_{2}={\frac {-b'-\delta '}{a}}\quad {\text{avec}}\quad \delta '^{2}=\Delta '=b'^{2}-ac}$

a) İlk olarak şu örnek denklemin çözümünü arayalım:

${\displaystyle 5x^{2}-5x+1=0\;}$

Çözüm iki kök bulunmasını gerektirir. Bu iki kökün x₁ ve x₂ olduğunu kabul edelim. Bu iki kökü, yani x₁ ve x₂ çözüm değerlerini bulmak için, şu Δ diskriminant ifadesi incelenir ve bu diskriminant değeri kuadratik denklem çözüm formülüne konulup şu iki gerçel kök bulunur::

${\displaystyle \Delta =(-5)^{2}-4\times 5\times 1=5\quad {\text{ ve }}\quad x_{1}={\frac {5+{\sqrt {5}}}{10}},\quad x_{2}={\frac {5-{\sqrt {5}}}{10}}.}$

b) İkinci örnek olarak verilen denklem şu olsun:

${\displaystyle x^{2}+6x+9=0}$

ve bunun diskriminant değeri sıfır olarak şöyle bulunur:

${\displaystyle \Delta =6^{2}-4(1)(9)=36-36=0\;}$

Bu demektir ki bu denklem çözümü birbirine eşit iki gerçel kök olur

${\displaystyle x^{2}+6x+9=(x+3)^{2}\;}$

Bu birbirine çakışık iki kök değeri -3 olur.

c) Son olarak örnek denklem şu olsun:

${\displaystyle x^{2}+x+1=0}$

Bu denklem işin diskriminant Δ değeri şu olur:

${\displaystyle \Delta =1^{2}-4(1)(1)=-3\;}$

yani Δ negatiftir. Bu halde denklemin gerçel sayılarla kökleri bulunmamaktadır. Fakat bu halde kompleks kökleri bulunabilir. Diskriminantın kare kökü i√3 olur ve burada i "sanal birim" operatörüdür. Bundan dolayı şu çözüm ortaya çıkar:

${\displaystyle \ \quad {\text{et}}\quad x_{1}=-{\frac {1}{2}}+i{\frac {\sqrt {3}}{2}},\quad x_{1}=-{\frac {1}{2}}-i{\frac {\sqrt {3}}{2}}}$

.

eğer kuadratik formun diskriminantı negatif ise, φ(x, y) = a ile tanımlanan R² noktaları ensamblı bir hiperboldur. Eğer a pozitif ise, mavi ile gösterilen eğriye benzer şekil alir. Eğer a negatif ise ortaya çıkan eğri yeşil eğri benzeridir. Eğer a sıfıra eşitse, hiperbol dejenere olur ve kırmızı eğri benzeri bir eğri oluşur.

Gerçel sayılar seti üzerinde, iki değişkenli (x ve y) iki boyutlu φ kuadratik formu şu formülle ifade edilir:

${\displaystyle \varphi (x,y)=ax^{2}+bxy+cy^{2}\quad {\text{ burada }}\quad a,b,c\in \mathbb {K} }$

Kuadratik form aynı zamanda bir matris ifade ile de gösterilebilir:

${\displaystyle \varphi (x,y)={\begin{pmatrix}x&y\end{pmatrix}}{\begin{pmatrix}a&{\frac {b}{2}}\\{\frac {b}{2}}&c\end{pmatrix}}{\begin{pmatrix}x\\y\end{pmatrix}}}$

Bu matris şeklinde ifadenin determinantinin açılması, daha önce diskriminant için verilen ifadeye, yani -1/4(b² - 4ac) ifadesine eşittir. Bir geçen matris P kullanarak yapılan bir baz değişmesi bu determinatın değerinde değişme yapar. Daha detaylı bir açıklama ile, yeni baz için değer eski baz ile P determinantının karesinin çarpımına eşittir ve determinantın işareti değişmeden aynı kalmaktadır. Bu analizin incelenmesi daha ayrıntılı bir maddede yapılmaktadır.

Bunun için iki boyutlu kuadratik formları için üç tane farklı tanımlama yapılmaktadır. B bazında olan kuadratik formun diskriminantı, B bazındaki kuadratik forma bağlı olan matrisin determinantı olur. Daha önceki hale benzer bir açıklama ve hesaplama ile kuadratik formun diskriminantının b² - 4ac ifadesine eşit olduğu tanımlanabilir. Sonra, kuadratik formun determinantına bağlı tek değişmez gibi, diskriminant da +1, 0 veya -1 değerleri alabilen determinant işareti olarak tanımlanır.

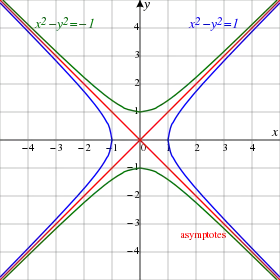
Diskriminant kuadratik formları üç tane değişik gruba ayırmaktadır. İki boyutta, kanonik bazda determinatın değerinin diskriminantı tanımlaması yapıldıktan sonra, eğer verilmiş bir a değeri icin diskriminantın işareti pozitif ise, φ(x, y) = a değişebilirinin (x, y) noktalarının E_a ensamblı bir elipse karşıttır veye ensambl boştur. Eğer diskriminant sıfır ise, bu halde E_a bir parabol'a karşıt olur. Eğer diskriminant negatif ise, E_a bir hiperbol olur. Kuadratik formlar üç farklı şekilde konik seksiyon elde etmeye izin verir.

• İkinci derece polinomlar için ve matris notasyonu kullanarak şu ifade ele geçirilir :

${\displaystyle \Delta (P)={\frac {(-1)^{\frac {2(2-1)}{2}}}{a}}{\begin{vmatrix}&a&2a&0&\\&b&b&2a&\\&c&0&b&\\\end{vmatrix}}=-{\begin{vmatrix}&1&2&0&\\&b&b&2a&\\&c&0&b&\\\end{vmatrix}}=-{\begin{vmatrix}b&2a&\\0&b&\\\end{vmatrix}}+2{\begin{vmatrix}b&2a&\\c&b&\\\end{vmatrix}}=b^{2}-4ac}$

• Üçüncü derecede polinomları için genellikle normalize edilmiş polinom, yani ana diagonal elemanlarının hepsi 1'e eşit olan matrix, kullanılır ve şu ifade ortaya çıkar:

${\displaystyle P=X^{3}+aX^{2}+bX+c\;}$

Bundan şu formül çıkartılır [1] :

${\displaystyle \Delta (P)=(-1)^{\frac {3(3-1)}{2}}{\begin{vmatrix}&1&a&b&c&0\\&0&1&a&b&c&\\&3&2b&c&0&0&\\&0&3&2b&c&0&\\&0&0&3&2b&c&\\\end{vmatrix}}=a^{2}b^{2}+18abc-4b^{3}-4a^{3}c-27c^{2}\;}$

Bu ifade epey karmaşık görünmektedir; fakat bunun bir uygun nedeni vardır. Geleneksel olarak bu karmaşık ifade kullanılırsa yapılan ikamelerle şu şeklide bir polinom elde edilebilir ve bunun diskriminantı gayet basittir:

${\displaystyle P=X^{3}+pX+q\quad {\text{et}}\quad \Delta (P)=-4p^{3}-27q^{2}\;}$

Gerçel katsayılı 3.derece polinom denklemi halinde, eğer diskriminant kesinlikle negatif ise denklemin üç tane ayrı değerde gerçel çözümü bulunur; eğer determinant sıfır ise üç tane birbirine çakışan tek bir gerçel değerde çözüm vardır ve eğer determinant kesinlikle pozitif ise tek bir gerçel çözüm bulunup diğer iki tane çözüm ise birbirlerine conjuge kompleks sayılardır.

• Elips eğrileri iki değişkenli üçüncü derece polinomların özel bir şeklinden ortaya çıkarlar.

Elipsin en basit bir halinde denklem şöyledir: ${\displaystyle y^{2}=x^{3}+ax+b}$ Bunda ${\displaystyle a,b}$ katsayıları gerçel sayılardır. Bu halde diskriminant şöyle tanımlanır: ${\displaystyle \Delta =-16(4a^{3}+27b^{2})}$.

P dereceli polinom için genel diskriminant ifadesi şöyle tanımlanır:

${\displaystyle P=a_{n}X^{n}+a_{n-1}X^{n-1}+\cdots +a_{1}X+a_{0}\;}$

ve bundan şu ortaya çıkar:

${\displaystyle \Delta (P)=(-1)^{\frac {n(n-1)}{2}}{\begin{vmatrix}1&0&\cdots &0&n&0&\cdots &0\\a_{n-1}&a_{n}&\ddots &\vdots &(n-1)a_{n-1}&na_{n}&\ddots &\vdots \\\vdots &a_{n-1}&\ddots &0&\vdots &(n-1)a_{n-1}&\ddots &0\\a_{0}&\vdots &\ddots &a_{n}&a_{0}&\vdots &\ddots &na_{n}\\0&a_{0}&&a_{n-1}&0&a_{0}&&(n-1)a_{n-1}\\\vdots &\ddots &\ddots &\vdots &\vdots &\ddots &\ddots &\vdots \\0&\cdots &0&a_{0}&0&\cdots &0&a_{0}\\\end{vmatrix}}}$