Çeyrekler açıklığı
Betimsel istatistikde çeyrekler açıklığı sıralanmış bir veri dizisinin orta yarısını (%50sini) kapsayan ve üçüncü dörttebirlik ve birinci dörttebirlik aralığını veya farkını (yani Q3 - Q1) gösteren bir istatistiksel yayılma ölçüsüdür. Birinci dörttebirlik sıralanmış veri dizisinin ilk %25inden büyük ve üçüncü dörttebirlik sıralanmış veri dizisinin %25inden daha küçük olduğu için, bu iki dörttebirlik arasında kalan veri yüzdesi %50dir. Çeyrekler açıklığı ölçüm birimi veri ölçüm birimi ile aynıdır. İngilizce'si IQR'dır (Inter Quantile Range).
Çeyrekler açıklığı sıralanmış veriler içinde aşırı küçük veya aşırı büyük uçsal değerlerden (yani aykırı değerlerden) etkilenmez. Özel bir istatistiksel terimle Çeyrekler açıklığı güçlü (en:robust) bir yayılma ölçüsüdür. Bu nedenle "istatistiksel yayılma" ölçüsü olarak açıklık'a tercih edilir. Eğer alışılagelen yayılma ölçüsü olarak genellikle kullanılan varyans veya standart sapma için mevcut olduğu bilinen dezavantajlar (ilk akla gelen; çarpıklık) pratik bir problem için sorun yaratıyorsa (örnegin veri dizisi içinde çok aşırı bir veya birkaç aykırı değer varsa) çeyrekler açıklığı varyans veya standart sapma ya da tercih edilir.
Örnekler
Tablo şeklinde veri ile
i x[i] Dörttebirlik 1 102 2 104 3 105 Q1 4 107 5 108 6 109 Q2 (medyan) 7 110 8 112 9 115 Q3 10 116 11 118
Bu tabloda verilmis veriler için "çeyrekler açıklığı"
- = = 115 − 105 = 10.
Veriler bir basit kutu grafiği ile verilirse
| |
| +-----+-+ |
o * |-------| | |---|
| +-----+-+ |
| |
+---+---+---+---+---+---+---+---+---+---+---+---+ Sayılar ekseni
0 1 2 3 4 5 6 7 8 9 10 11 12
Bu veri seti için
- birinci (alt) dörttebirlik (, ) = 7
- medyan (ikinci dörttebirlik) (, ) = 8.5
- üçüncü (üst) dörttebirlik (, ) = 9
- çeyrekler açıklığı,
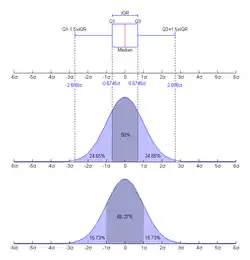
Olasılık dağılımları için çeyrekler açıklığı
Bir sürekli olasılık dağılımı için çeyrekler açıklığı, önce cebirsel olarak, olasılık yoğunluk fonksiyonunun integralini alarak hesaplanir ve bu yığmalı dağılım fonksiyonunu verir. Yığmalı dağılım fonksiyonunun negatif sonsuz (-∞) değerden 0,25 değere kadar bulunan integral değeri birinci dörttebirliği verir. Yine negatif sonsuzdan (-∞) 0,75 değere kadar alınan integral ise dörttebirliği verir. Bunlar formüller halinde şöyle ifade edilir:
Burada Q1: birinci dörttebirlik, Q3: üçüncü dörttebirlik ve CDF:yığmalı dağılım fonksiyonu olur.
Ancak birçok sürekli olasılık dağılımı için olasılık yoğunluk fonksiyonunun integralını almanın çok zor olduğu bilinmektedir. Herhangi başka bir yöntemle yığmalı dağılım fonksiyonu da bulunabilirse de uygun olur. Bir başka yöntem olarak yığmalı dağılım gösterimi kullanılabilir. Eğer gösterim çok iyi ve uygun ölçekli yapılmış ise, gösterimsel olarak da yığmalı olasılık dağılımı eğrisi üzerinde dörttebirlikler hemen bulunabilir.
Bazı olasılık dağılımları için medyan ve çeyrekler açıklığı değerleri şunlardır:
| Dağılım | Medyan | Çeyrekler açıklığı |
|---|---|---|
| Normal dağılım | μ | 2 Φ−1(0.75) ≈ 1.349 |
| Laplace dağılımı | μ | 2b ln(2) |
| Cauchy dağılımı | μ |
