Helmholtz bobini
Helmholtz bobini tekdüze manyetik alanı üretmeye yarayan bir alettir. Adını Alman fizikçi Hermann von Helmholtz’dan almıştır. Helmholtz bobini aynı eksendeki iki solenoid elektromıknatısından oluşur. Elektromanyetik alan oluşturmalarının yanı sıra, Helmholtz bobini aynı zamanda dış manyetik alanı nötrleştirmek için de kullanılır. Dünyanın manyetik alanı buna örnektir.

Tanım
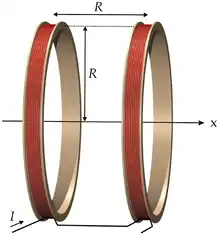
Helmholtz bobini solenoid diye adlandırılan iki özdeş dairesel manyetik bobinden oluşur. Helmholtz bobinini oluşturabilmek için solenoidler aynı eksene simetrik olarak yerleştirilip, yarıçap 'ye eşit olacak şekilde uzaklığında birbirinden ayrılır. Her iki bobin de aynı doğrultuda eşit miktarda elektrik akımı elde eder.
Bobinlerin merkezindeki manyetik alan farklılığını en aza indirmek için olarak kabul edilir ama bobinlerin merkezleri ve düzlemler arasındaki alan şiddetlerinde %7 oranında değişim vardır. Biraz daha büyük olan değeri, düzlem ve merkezler arasında kalan alanlardaki farklılık oranını düşürür.
Birkaç uygulamada, Dünya'nın manyetik alanını nötrleştirmek için kullanılan Helmholtz bobini, sıfıra çok yakın bir manyetik alan şiddeti üretir.
Matematik
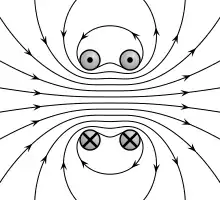
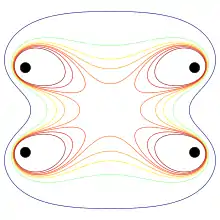
Uzayda herhangi bir noktadaki kesin manyetik alan hesabı, matematiksel olarak karışık olmakla birlikte Bessel fonksiyonunun uygulama alanına girer. Bobin çifti boyunca olan eksen baz alındığında hesaplama daha kolaylaşır ve alan şiddetinin Taylor serisi genişlemesiyle bulunan ve eksen boyunca bobin çiftlerinin merkez noktalarında uzaklıklarını mesafesi olarak alınması uygundur. Simetrik olarak, genişlemedeki tek mertebe terimleri sıfırdır. Orijin noktası alan şiddeti için büküm noktası olabilsin diye, bir tane bobinin terimi aynı zamanda 0 olmalıdır ve bunun için öncülük eden ve sabit olmayan terimi kullanılır. Basit bobin için büküm noktası kendi merkezine kadar mesafede bobin ekseni doğrultusunda konumu belirlenir. Böylece iki bobinin konumu şeklinde belirlenir.
Merkez noktasındaki manyetik alanının kesin değeri aşağıda ayrıntılı olarak verilmiştir. (Yarıçap = R, bobin sayısı = n, bobinlerin akımı =I , manyetik akı yoğunluğu = B)
boşluğun geçirgenliğidir. ().
Türev
Tek telli döngünün oluşturduğu eksenüstü alan için oluşturulan formülle başlanır. (Biot-savart yasası
- = geçirgenlik sabiti =
- = bobibin akımı, amper
- = bobinin yarıçapı, metre
- = bobin uzaklığı, metre
Helmholtz bobini n tane sarım sayısı içerir.
Orta noktadaki alan şiddeti:
Bir tane bobin yerine iki tane bobin de olabilir. (Birinci bobin, x=0 noktasındaki bobindir; ikinci bobin ise, x=R noktasındaki bobindir.) Simetriden dolayı, orta noktadaki alan şiddeti tek bobinin oluşturduğu değerin iki katı kadar olacaktır.
Maxwell bobini
Bobinlerin uzayda oluşturduğu alanın özdeşliklerini arttırabilmek amacıyla, ek bobinler dışarıdan eklenebilir. 1873 yılında James Clerk Maxwell, iki Helmholtz bobininin arasına daha büyük çaplı bir bobin yerleştirmiştir ve alan sapmalarını azaltan bu bobine bazen Maxwell bobini de denir.
Kaynakça
- https://en.wikipedia.org/wiki/Helmholtz_coil 4 Mart 2015 tarihinde Wayback Machine sitesinde arşivlendi.
- http://www.lightandmatter.com/html_books/0sn/ch11/ch11.html 3 Haziran 2011 tarihinde Wayback Machine sitesinde arşivlendi.
- http://circuitcellar.com/library/print/0606/Wotiz191/5.htm
- http://hyperphysics.phy-astr.gsu.edu/HBASE/magnetic/curloo.html#c3 17 Ekim 2018 tarihinde Wayback Machine sitesinde arşivlendi.
- http://radphys4.c.u-tokyo.ac.jp/asacusa/wiki/index.php?Cusp%20trap 20 Ocak 2015 tarihinde Wayback Machine sitesinde arşivlendi.
