Standartlaştırma
Standart skor, bir degerin normal dagilimda gerceklesme olasiligini bulmamizi saglayan ya da farkli popülasyonlardan gelen iki ornegi karsilastirmamizi saglayan bir standart sapma turudur. Standard skor eksi ya da arti deger alabilir; eksi ya da arti elimizde degerin aritmetik degerin altinda ya da ustunde oldugunu gosterir. Z-skoru temel bir standard skor turudur (aritmetik ortalama = 0.0 ve standard sapma 1.0). Standart skor, istenilen degerin ve popülasyon aritmetik ortalamasinin farkinin, popülasyon standard sapmasina bolunmesiyle elde edilir. Bu donusturme islemine, standardlastirma ya da normellestirme denir.
Standard skor, z-skoru, z-degeri ya da normal skor olarak da tabir edilebilir, hepsi ayni anlama gelir. Normal dagilim ve z dagilimi ayni seylerdir. Z-skoru donusumu eger popülasyon parametreleri biliniyorsa kullanilir. Eger elimizde sadece ornek degerleri varsa, t-istatistigini kullaniriz.
Hesaplanmasi
Bilinen x sayisini z standard skoruna cevirmek asagidaki formul kullanilir:
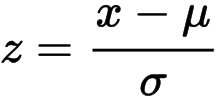
x: donusturulmek istenen herhangi bir deger
- μ: popülasyon aritmetik ortalamasi
- σ: popülasyon standart sapmasi
Formulu kullanarak bulunan z-skorunun mutlak degeri elimizdeki x degeri ile popülasyon aritmetik ortalamasi arasindaki uzakligin standart sapma biriminde karsiligidir. Negatif z-skoru elimizdeki x degerinin popülasyon aritmetik ortalamasi altinda, pozitif z-skoru ise ustunde oldugunu gosterir. Z-skorunu hesaplayabilmek icin popülasyonun standart sapma ve artimetik ortalama degerlinin bilinmesi gerekir, orneklerin istatistik bilgileri bulunmaz. Bir popülasyonun gercek standard sapmasini bulabilmek standard sinavlar (YGS, LGS gibi) haricinde imkansizdir. Popülasyondaki her bireyin bilgisinin toplanmasinin imkansiz oldugu durumlarda (cogunlukla), standart sapma rassal yontemle olusturulan ornekle hesaplanabilir.
T-skoru
T-skoru, z-skorlarinin 50 otelenmis halindeki bir standart skordur. Aritmetik ortalamasi 50 ve standart sapmasi 10'dur.
