Ağırlık merkezi

Bir cismin moleküllerine etki eden yerçekimi kuvvetlerinin bileşkesinin uygulama noktasına ağırlık merkezi denir. Fizikte ve mühendislik hesaplarında işlemlerin basitleştirilmesi için yaygın olarak kullanılır.

O , dikdörtgenin ağırlık merkezi.

Ağırlık Merkezinin Bulunması

Homojen yapılı ve simetrik cisimlerde ağırlık merkezi simetri eksenlerinin kesişme noktasındadır. Basit geometrik şekillerin veya basit geometrik şekillere bölünebilen cisimlerin ağırlık merkezleri çizim yolu ile kolaylıkla bulunabilir.

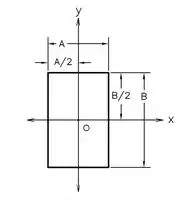
Yandaki şekilde , bir dirkdörtgenin ağırlık merkezinin , birbirine dik iki kenarın ortalarını birleştirmek sureti ile çizilen doğruların kesişme noktalarının verdiği O noktası olduğu gösterilmiştir. Bu nokta aynı zamanda dikdörtgenin köşegenlerinin de kesişim noktasıdır.

Ağırlık Merkezinin Çizim Yoluyla Bulunması

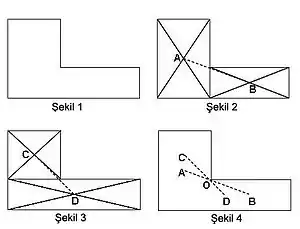
İki dikdörtgenden oluşan bir cismin ağırlık merkezi.

Yandaki şekillerde iki dikdörtgenden oluşan bir cismin ağırlık merkezinin çizim yoluyla bulunuşu gösterilmektedir.

Cisim şekil 2'de görüldüğü biçimde iki dikdörtgene ayrılır ve oluşan iki yeni dikdörgenin köşegenleri çizilerek, bu dikdörtgenlerin A ve B ağırlık merkezleri bulunur. İki dikdörtgenden oluşan bu cismin ağırlık merkezi AB doğrusu üzerinde olacaktır. Ancak tam yeri belli değildir.
Şekil 3'te görüldüğü biçimde cisim iki farklı dikdörtgene daha ayrılır, köşegenleri çizilerek C ve D ağırlık merkezleri bulunur. Yine iki dikdörtgenden oluşan bu cismin ağırlık merkezi CD doğrusu üzerinde olacaktır.
Şekil 4'te görülen biçimde, AB ve CD doğruları kesiştirilir, kesişme noktası olan O noktası cismin ağırlık merkezidir.

Ağırlık Merkezinin Hesap Yoluyla Bulunması

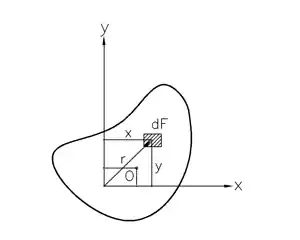
Herhangi n sayıda parçadan oluşan homojen düzlemsel bir cismin, seçilen bir eksen takımına göre ağırlık merkezi yeri olan ( $X_{o}$ , $Y_{o}$ ) noktası aşağıdaki bağıntılar yardımıyla hesaplanabilir. Burada ; $F_{i}$ parça alanı , $x_{i}$ parçanın x koordinatı , $y_{i}$ parçanın y koordinatıdır.

Ağırlık merkezinin hesabı

$X_{1}0=\sum _{i=1}^{n}{\frac {F_{i}\cdot x_{i}}{\sum F}}$ , $Y_{o}=\sum _{i=1}^{n}{\frac {F_{i}\cdot y_{i}}{\sum F}}$

Burada ayrica,

$S_{x}=\sum _{i=1}^{n}{F_{i}\cdot x_{i}}$ , $S_{y}=\sum _{i=1}^{n}{F_{i}\cdot y_{i}}$

ya da integral biçimleriyle,

$S_{x}=\int _{F}y\cdot dF$ , $S_{y}=\int _{F}x\cdot dF$

büyüklükleri statik momentler olarak tanımlanır, statik momentin birimi cm³'dür . Görüleceği üzere ağırlık merkezi koordinatları, ilgili eksen için statik momentin alana bölümüdür.

Ağırlık merkezinin hesabının daha genel hali aşağıdaki biçimdedir. Karmaşık geometrik şekillerin ağırlık merkezleri bu integraller yardımıyla hesaplanır.

$X_{o}={\frac {1}{F}}\int _{F}y\cdot dF$ , $Y_{o}={\frac {1}{F}}\int _{F}x\cdot dF$

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.