Çarpanlara ayırma
Çarpanlara ayırma, bir polinomun, tam sayının ya da matrisin kendisini oluşturan bileşenlerin çarpımı şeklinde yazılmasıdır. Örneğin 15 sayısı 3 ve 5 asal sayılarının çarpımı şeklinde yazılabilir: 3 × 5, ya da x2 − 4 polinomu (x − 2)(x + 2) şeklinde yazılabilir.
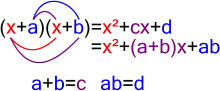
Çarpanlara ayırmadaki temel amaç bir bütünü daha küçük yapılara ayırmaktır; sayıları asal sayıların çarpımı, polinomları indirgenemeyen polinomların çarpımı şeklinde yazmak gibi. Çarpanlara ayırmanın tersi genişletmedir.
Asal çarpanlarına ayırma çok büyük sayılar için zor bir problemdir. Bu problemin bilinen bir çözümü yoktur. Bu yüzden RSA gibi açık anahtarlı şifreleme yöntemlerinde kullanılır.
Tam sayılar
Aritmetiğin temel teoremine göre 1'den büyük her tam sayı asal sayıların çarpımı şeklinde yazılabilir.
Polinomlar
Karesel polinomlar
şeklindeki her karesel polinom,
- şeklinde çarpanlarına ayrılabilir.
Karesel özdeşlikler
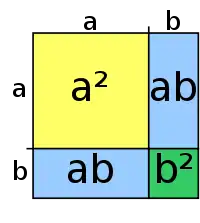
Aşağıdaki özdeşlikler kullanılarak bazı polinomlar kolayca çarpanlarına ayrılabilir.
ve
Örneğin,
İki kare toplamı/farkı
İki kare farkı,
Eğer iki kare toplam halindeyse karmaşık sayı cinsinden çarpanlarına ayrılır,
Gruplandırarak çarpanlara ayırma
Birden çok değişkenin olduğu bir ifadede önce benzer terimler bir araya getirilip ortak çarpan parantezine alınır, ardından oluşan diğer ortak terim de paranteze alınır. Örneğin,
Benzer terimler bir araya getirlir,
Ortak çarpan parantezine alınır,
Oluşan yeni ortak terim de paranteze alınır
Dış bağlantılar
- Wolfram Alpha, polinomları ve sayıları çarpanalarına ayırır.28 Mart 2019 tarihinde Wayback Machine sitesinde arşivlendi.
