Esnek olmayan çarpışma

Esnek olmayan çarpışmalar, esnek çarpışmaların aksine, sürtünme nedeniyle kinetik enerjinin korunmadığı bir çarpışma çeşididir.

Stroboskopik flaşla bir saniyede 25 görüntüsü çekilen zıplayan top. Topun yerle çarpışması esnek olmayan bir çarpışma, yani top her zıplayışında enerji kaybeden bir çarpışma gerçekleşir. Hava sürtünmesini ihmal ettiğimizde, topun her zıplayışında oluşan yüksekliğin oranının kare kökü bize top/yüzey etkisi için eski haline dönme katsayısını verir.

Makroskopik cisimlerin çarpışmalarında, kinetik enerjinin bir kısmı, cisimlerin deforme olduğu ve ısıya neden olan, atomlar arasında meydana gelen titreşim enerjisine dönüşür.

Sıvı ve gaz molekülleri nadirende olsa tam anlamıyla mükemmel esnek çarpışma yaparlar çünkü her çarpışmayla birlikte moleküllerin içinde ve öteleme hareketleri arasında kinetik enerji değişimi yaşanır. Herhangi bir anda, çarpışmaların yarı yarıya değişen oranında; bir yarısı esnek olmayan çarpışma (çarpışma öncesi sahip olduğu kinetik enerjiye nazaran çarpışma sonrasında daha az kinetik enerjiye sahip olan çarpışmalar), ve diğer yarısı da mükemmel derecede esnek olan çarpışmalar (çarpışma öncesi sahip olduğu kinetik enerji kadar çarpışma sonrasında da aynı kinetik enerjiye sahip olan çarpışmalar) olur.

Esnek olmayan çarpışmalarda kinetik enerji korunmaz ama momentumun korunduğundan söz edilebilir.[1] Basit balistik bir sarkaç probleminde, kinetik enerjinin korunumu durumu sadece ve sadece blok en büyük açısıyla sallandığında gerçekleşir.

Nükleer fiziğinde, esnek olmayan çarpışma atom altı parçacığın atom çekirdeğinde bozulmaya neden olan çarpışmalardan bir tanesidir. Derin esnek olmayan saçılma Rutherford atomu içine problanmış hemen hemen aynı şekilde atomik parçacıkların yapısını tarama yöntemidir (bakınız Rutherford scattering). 1960’ların sonlarında bu tür deneyler protonlar üzerinde Stanford doğrusal hızlandırıcıda (SLAC) yüksek enerjili elektronlar kullanılarak gerçekleştirilmiştir. Rutherford saçılmasında olduğu gibi, proton hedefleriyle elektronların derin esnek olmayan saçılması çok az etkileşim içinde olan ve az sayıda miktarı geri zıplayan elektronları ortaya çıkardı. Bu protondaki yüklerin küçük parçacıklar içinde yoğunlaştığını gösterir, ve Rutherford’un teorisine göre de, pozitif yükler atomun içinde çekirdekte yoğunlaşırlar. Ama, proton halinde, kuarkların yükleri bir değil üç farklı konsantrasyonda olur.

Formüller

Bir boyutta esnek olmayan çarpışmadan sonraki hızlarının formulü:

v_{a}={\frac {C_{R}m_{b}(u_{b}-u_{a})+m_{a}u_{a}+m_{b}u_{b}}{m_{a}+m_{b}}}

v_{b}={\frac {C_{R}m_{a}(u_{a}-u_{b})+m_{a}u_{a}+m_{b}u_{b}}{m_{a}+m_{b}}}

v_a çarpışmadan sonraki ilk nesnenin son hızı

v_b çarpışmadan sonraki ikinci nesnenin son hızı

u_a çarpışmadan önceki ilk nesnenin ilk hızı

u_b çarpışmadan önceki ikinci nesnenin ilk hızı

m_a ilk nesnenin kütlesi

m_b ikinci nesnenin kütlesi

C_R eski haline dönme katsayısı eğer 1 ise, esnek bir çarpışmaya sahip oluruz; eski haline dönme katsayısı eğer 0 ise tamamen esnek olmayan çarpışmaya sahip oluruz.

Momentumun merkezi çerçevesine gore, formüller şu şekilde indirgenebilir:

v_{a}=-C_{R}u_{a}

v_{b}=-C_{R}u_{b}

İki ve üç boyutta çarpışmalar için, bu formüllerdeki hızların bileşenleri temas ettikleri noktadaki teğet düzlemine diktir.

Esnek olmayan çarpışma örnekleri

Bir lastik topun katı bir yüzeyle çarpışması, gibi çarpışan cisim diğerine yapışıp kalmıyor ama biraz kinetik enerji kaybediyorsa çarpışma esnek olmayan çarpışmadır. Örneğin lastik top katı yüzeyle çarpıştığında, çarpışma inelastiktir çünkü top şekil değiştirmiş ve kinetik enerji kaybetmiştir.

Tamamen esnek olmayan çarpışma

Tamamen esnek olmayan çarpışma kinetik enerji maksimum oranda kaybedildiğinde gerçekleşir. Tamamen esnek olmayan çarpışmada, yani eski haline dönme katsayısı 0 iken, çarpışan cisimler birbirlerine yapışırlar. Bu tip bir çarpışmada, iki cismin birbirine yapışmasıyla kinetik enerji kaybedilir. Bu birbirlerine bağlanma enerjisi genellikle sistemde maksimum kinetik enerjinin kaybedilmesiyle meydana gelir. Bu noktada momentumun korunumunu da düşünmek gerekir: (Not: yukarıda birbirlerine çarpan blok örneğinde de olduğu gibi, iki cisimli sistemin momentumu yalnızca yüzey sürtünmesizse korunur. Sürtünmeyle birlikte, iki cismin momentumu birbirlerine çarptıkları noktadaki yüzeye aktarılır. Benzer şekilde, eğer hava sürtünmesi varsa, cisimlerin momentumu havaya aktarılır. Aşağıdaki eşitlikler üstteki A cismi ve B cisminin oluşturduğu iki cisimli sistem için geçerlidir. Bu örnekte, sistemin momentum korunur çünkü yüzey ve çarpışan cisimler arasında herhangi bir sürtünme yoktur.

m_{a}u_{a}+m_{b}u_{b}=\left(m_{a}+m_{b}\right)v\,

v son hız, ve formülü şudur:

v={\frac {m_{a}u_{a}+m_{b}u_{b}}{m_{a}+m_{b}}}

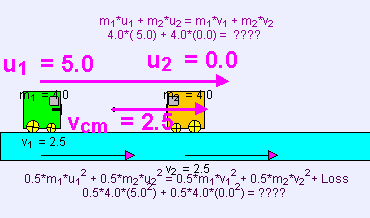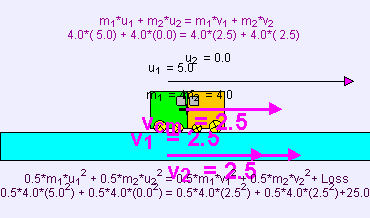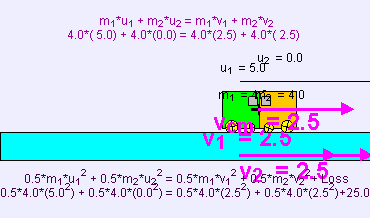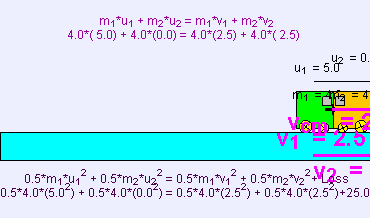
Toplam kinetik enerjinin indirgenmiş hali iki parçacıklı bir sistemi referans aldığımızda momentum noktasının merkezindeki çarpışmadan önceki toplam kinetik enerjiye eşittir, çünkü böyle bir durumda çarpışmadan sonra kinetik enerji sıfıra eşit olur. Bu durumda, çarpışmadan önceki kinetik enerjinin çoğu daha küçük kütleye sahip olan parçacığa aittir. Başka bir referans noktasında, kinetik enerjinin indirgenmesine ek olarak, kinetik enerjinin bir parçacıktan diğer parçacığa transferi gerçekleşir; bu çerçevede bağlı olması ne kadar göreceli olduğunu gösterir.

Zamanla ters olarak, birbirinden gittikçe uzaklaşan iki nesne durumuna sahibiz, örneğin Tsiolkovsky roket eşitliğiyle karşılaştırılarak, rokete itme uygulandığında, ya da atış yapıldığında.

Tamamen esnek olmayan çarpışma örneği

Bir meteor taşının yere çarpışında olduğu gibi, çarpışan cisimlerin çarpışmadan sonra birlikte hareket ettiği çarpışma, tamamen esnek olmayan çarpışma olarak adlandırılır. Örneğin lastik hareket ettiği çarpışma tamamen esnek olmayan çarpışmadır.Tamamen esnek olmayan çarpışmada çarpışmadan sonra cisimler birbirlerine yapışarak hareketlerine devam ederler. Çarpışmadan önceki toplam momentum, çarpışmadan sonraki birleşik sistemin toplam momentumuna eşit olur.

Kısmen esnek olmayan çarpışma

Kısmen esnek olmayan çarpışma gerçek dünyada olan çarpışmaların en yaygın olan türüdür. Bu tip çarpışmalarda, nesneler birbirlerine yapışmazlar, ama kinetik enerjinin bir kısmı kaybedilir. Kısmen esnek olmayan çarpışmada kinetik enerjinin bir kısmı sürtünme, ses ve ısıya dönüşür.

Kaynakça

Ferdinand Beer, Jr. and E. Russell Johnston (1996). Vector equations for engineers: Dynamics. Sixth. McGraw Hill. ss. 794-797. ISBN 978-0070053663. Eğer etki eden dış kuvvetlerin toplamı sıfır ise ... parçacığın toplam momentum korunur.. Eğer etkinin genel durumundan bahsedecek olursak, örneğin, e 1’e eşit olmadığında, parçacığın toplam enerjisi korunmaz.

Dış bağlantılar

Petit, Regis. "The Art of Billiards Play". 31 Aralık 2012 tarihinde kaynağından arşivlendi. Erişim tarihi: 30 Temmuz 2012. Gives the general vector equations of a collision between two bodies of any speed.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Ferdinand Beer, Jr. and E. Russell Johnston (1996). Vector equations for engineers: Dynamics. Sixth. McGraw Hill. ss. 794-797. ISBN 978-0070053663. Eğer etki eden dış kuvvetlerin toplamı sıfır ise ... parçacığın toplam momentum korunur.. Eğer etkinin genel durumundan bahsedecek olursak, örneğin, e 1’e eşit olmadığında, parçacığın toplam enerjisi korunmaz.